题目内容
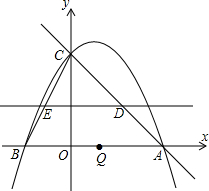 如图,抛物线y=ax2+bx+c交x轴于A(4,0),B(-2,0)两点,交y轴于点C(0,4).
如图,抛物线y=ax2+bx+c交x轴于A(4,0),B(-2,0)两点,交y轴于点C(0,4).(1)求该抛物线的解析式;
(2)若动点Q从点B出发,以每秒2个单位长度沿线段BA方向运动,同时动直线l从x轴出发,以每秒1个单位长度沿y轴方向平行移动,直线l交AC与D,交BC于E,当点Q运动到A点时,两者都停止运动.设运动时间为t秒.△QOD的面积为S.
①写出S与t的函数关系式,并求S=
| 1 |
| 2 |
②在点Q及直线l的运动过程中,是否存在t的值使∠EQD=90°?若存在,请求t的值;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)将已知三点的坐标代入到二次函数的解析式,利用待定系数法确定二次函数的解析式即可;
(2)①根据题意,得:BQ=2t,yE=yD=t,S△BDC=
BO•OC=
×2×4=4,然后求得s与t的函数关系式,从而得到有关t的方程,然后求解即可;
②若∠DQE=90°时,过点D作DF⊥AB于F,过点E作EG⊥AB于G,利用△BGE∽△BOC表示出QG=2t-
=
、AF=t,DF=t,QF=AB-BQ-AF=6-2t-t=6-3t,然后利用△EGQ∽△QDF列出比例式求得t值即可.
(2)①根据题意,得:BQ=2t,yE=yD=t,S△BDC=
| 1 |
| 2 |
| 1 |
| 2 |
②若∠DQE=90°时,过点D作DF⊥AB于F,过点E作EG⊥AB于G,利用△BGE∽△BOC表示出QG=2t-
| t |
| 2 |
| 3t |
| 2 |
解答: 解:(1)把点A(4,0),B(-2,0),C(0,4)代入抛物线y=ax2+bx+c得:
解:(1)把点A(4,0),B(-2,0),C(0,4)代入抛物线y=ax2+bx+c得:
,
解得
∴二次函数的解析式为:y=-
x2+x+4;
(2)由题意,得:BQ=2t,yE=yD=t,S△BDC=
BO•OC=
×2×4=4,
①s与t的函数关系式为
Ⅰ当0≤t<1时,-t2+t=2
整理得:t2-t+2=0,次方程无实数根;
Ⅱ当1≤t≤3时,t2-t=2
解得:t=2或t=-1,
综上,t=2;
②存在.若∠DQE=90°时,过点D作DF⊥AB于F,过点E作EG⊥AB于G,则△BGE∽△BOC,
∴
=
,
∴BG=
=
=
,
∴QG=2t-
=
.
同理可求AF=t,DF=t,QF=AB-BQ-AF=6-2t-t=6-3t,
易得△EGQ∽△QDF,
∴
=
∴
=
,
∴t=
.
 解:(1)把点A(4,0),B(-2,0),C(0,4)代入抛物线y=ax2+bx+c得:
解:(1)把点A(4,0),B(-2,0),C(0,4)代入抛物线y=ax2+bx+c得:
|
解得
|
∴二次函数的解析式为:y=-
| 1 |
| 2 |
(2)由题意,得:BQ=2t,yE=yD=t,S△BDC=
| 1 |
| 2 |
| 1 |
| 2 |
①s与t的函数关系式为
|
Ⅰ当0≤t<1时,-t2+t=2
整理得:t2-t+2=0,次方程无实数根;
Ⅱ当1≤t≤3时,t2-t=2
解得:t=2或t=-1,
综上,t=2;
②存在.若∠DQE=90°时,过点D作DF⊥AB于F,过点E作EG⊥AB于G,则△BGE∽△BOC,
∴
| GB |
| OB |
| GE |
| OC |
∴BG=
| OB•EG |
| OC |
| 2t |
| 4 |
| t |
| 2 |
∴QG=2t-
| t |
| 2 |
| 3t |
| 2 |
同理可求AF=t,DF=t,QF=AB-BQ-AF=6-2t-t=6-3t,
易得△EGQ∽△QDF,
∴
| EG |
| QF |
| QG |
| DF |
∴
| t |
| 6-3t |
| ||
| t |
∴t=
| 18 |
| 11 |
点评:本题考查了二次函数的综合题型,其中涉及到的知识点有待定系数法和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
相关题目
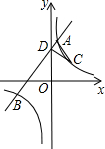 如图,已知直线y=mx+b与双曲线y=
如图,已知直线y=mx+b与双曲线y=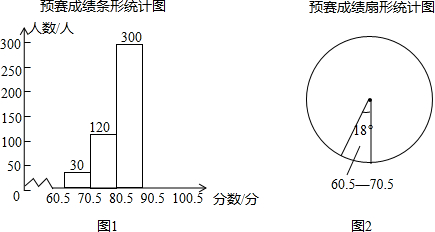

 阅读下面的材料:
阅读下面的材料: 如图,⊙O是以原点为圆心,
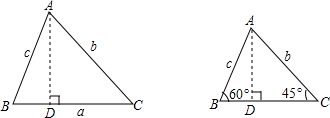
如图,⊙O是以原点为圆心,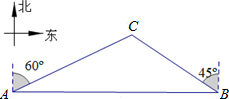 如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里/小时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我领海区域的C处截获可疑渔船,问我渔政船的航行路程是多少海里?(结果精确到0.1海里,
如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里/小时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我领海区域的C处截获可疑渔船,问我渔政船的航行路程是多少海里?(结果精确到0.1海里,