题目内容
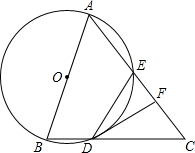 如图,已知AB=AC,以AB为直径的⊙O分别交BC,AC于D,E两点,F为CE的中点,连接DF,DE.
如图,已知AB=AC,以AB为直径的⊙O分别交BC,AC于D,E两点,F为CE的中点,连接DF,DE.(1)求证:△DEF为等腰三角形;
(2)判断DF与⊙O的位置关系并说明理由.
考点:切线的判定,等腰三角形的判定与性质
专题:证明题
分析:(1)根据等腰三角形的性质,由AB=AC得∠B=∠C,再根据圆内接四边形的性质得∠DEC=∠B,则∠DEC=∠C,于是根据等腰三角形的判定定理即可得到结论;
(2)连结OD、AD,如图,先根据圆周角定理得∠ADB=90°,在利用等腰三角形的性质得BD=CD,于是判定OD为△ABC的中位线,则OD∥AC,接着根据等腰三角形的性质,由△DEC为等腰三角形,F为CE的中点得到DF⊥CE,所以OD⊥DF,然后根据切线的判定定理即可得到DF为⊙O的切线.
(2)连结OD、AD,如图,先根据圆周角定理得∠ADB=90°,在利用等腰三角形的性质得BD=CD,于是判定OD为△ABC的中位线,则OD∥AC,接着根据等腰三角形的性质,由△DEC为等腰三角形,F为CE的中点得到DF⊥CE,所以OD⊥DF,然后根据切线的判定定理即可得到DF为⊙O的切线.
解答:(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠DEC=∠B,
∴∠DEC=∠C,
∴△DEC为等腰三角形;
(2)解:DF与⊙O相切.理由如下:
连结OD、AD,如图,
∵AB为直径,
∴∠ADB=90°,
∵AB=AC,
∴BD=CD,
∵OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵△DEC为等腰三角形,F为CE的中点,
∴DF⊥CE,
∴OD⊥DF,
∴DF为⊙O的切线.
∴∠B=∠C,
∵∠DEC=∠B,
∴∠DEC=∠C,
∴△DEC为等腰三角形;
(2)解:DF与⊙O相切.理由如下:

连结OD、AD,如图,
∵AB为直径,
∴∠ADB=90°,
∵AB=AC,
∴BD=CD,
∵OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵△DEC为等腰三角形,F为CE的中点,
∴DF⊥CE,
∴OD⊥DF,
∴DF为⊙O的切线.
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了等腰三角形的判定与性质.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
化简
÷(1+
)的结果是( )
| a+1 |
| a2-2a+1 |
| 2 |
| a-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
二次函数y=-
x2+
x+1000的图象经过第一象限的整格点(即纵、横坐标是正整数的点) 共有( )个.
| 1 |
| 2 |
| 1999 |
| 2 |
| A、1 000 |
| B、1 001 |
| C、1 999 |
| D、2 001 |
 如图,直线AB,CD,EF相交于点O,EF⊥AB,OG平分∠COF,若∠COG:∠BOC=1:7,求∠DOF的大小.
如图,直线AB,CD,EF相交于点O,EF⊥AB,OG平分∠COF,若∠COG:∠BOC=1:7,求∠DOF的大小.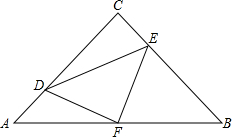 如图,在Rt△ABC中,AC=BC,∠C=90°,AB=8,点F是AB边的中点,点D、E分别在AC、BC边上运动,且保持AD=CE,连接DE、DF、EF.在此运动变化的过程中,下列结论中正确的结论是
如图,在Rt△ABC中,AC=BC,∠C=90°,AB=8,点F是AB边的中点,点D、E分别在AC、BC边上运动,且保持AD=CE,连接DE、DF、EF.在此运动变化的过程中,下列结论中正确的结论是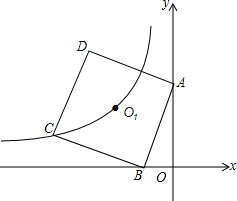 如图,B(-1,0),正方形ABCD中心为O,双曲线y=
如图,B(-1,0),正方形ABCD中心为O,双曲线y= 如图,OA⊥OB,CO⊥DO,
如图,OA⊥OB,CO⊥DO,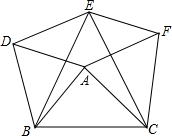 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF,
如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF,