题目内容
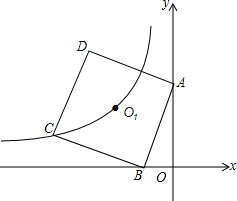 如图,B(-1,0),正方形ABCD中心为O,双曲线y=
如图,B(-1,0),正方形ABCD中心为O,双曲线y=| k |
| x |
考点:反比例函数图象上点的坐标特征
专题:
分析:作CE⊥x轴于E,连接AC,先求得△EBC≌△OAB,得出CE=OB=1,BE=OA,进而求得C点的坐标为(k,1),进一步求得A的坐标,从而求得O1(
,-
),代入y=
即可求得k的值.
| k |
| 2 |
| k |
| 2 |
| k |
| x |
解答: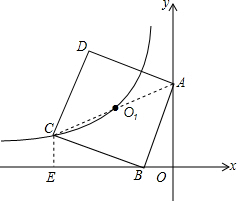 解:作CE⊥x轴于E,连接AC,
解:作CE⊥x轴于E,连接AC,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵∠EBC+∠ABO=∠BAO+∠ABO=90°,
∴∠EBC=∠BAO,
在△EBC和△OAB中,
,
∴△EBC≌△OAB(AAS),
∴CE=OB=1,BE=OA,
∴C的纵坐标为1,
代入y=
求得x=k,
∴C(k,1)
∴OE=-k,
∴OA=BE=-k-1,
∴A(0,-k-1),
∴O1(
,-
),
代入y=
求得k=-4.
 解:作CE⊥x轴于E,连接AC,
解:作CE⊥x轴于E,连接AC,∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵∠EBC+∠ABO=∠BAO+∠ABO=90°,
∴∠EBC=∠BAO,
在△EBC和△OAB中,
|
∴△EBC≌△OAB(AAS),
∴CE=OB=1,BE=OA,
∴C的纵坐标为1,
代入y=
| k |
| x |
∴C(k,1)
∴OE=-k,
∴OA=BE=-k-1,
∴A(0,-k-1),
∴O1(
| k |
| 2 |
| k |
| 2 |
代入y=
| k |
| x |
点评:本题考查了反比例函数图象上的坐标特征,正方形的性质,表示出点C、A的坐标是解题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 若实数a、b、c在数轴上对应点的位置如图所示,则|c|-|b-a|+|b+c|等于( )
若实数a、b、c在数轴上对应点的位置如图所示,则|c|-|b-a|+|b+c|等于( )| A、-a | B、-a+2b |
| C、-a-2c | D、a-2b |
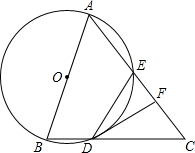 如图,已知AB=AC,以AB为直径的⊙O分别交BC,AC于D,E两点,F为CE的中点,连接DF,DE.
如图,已知AB=AC,以AB为直径的⊙O分别交BC,AC于D,E两点,F为CE的中点,连接DF,DE. 已知 四边形ABCD中,∠ABD=∠CBD=∠ACD=30°,BE=4,DE=2,则S△ABC=
已知 四边形ABCD中,∠ABD=∠CBD=∠ACD=30°,BE=4,DE=2,则S△ABC= 如图,直线AB、CD相交于点O,DM⊥AB,若∠1=∠2,求∠CON的度数.
如图,直线AB、CD相交于点O,DM⊥AB,若∠1=∠2,求∠CON的度数.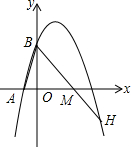 抛物线y=-
抛物线y=- 如图,?OABC的顶点O在坐标原点,顶点A、C在反比例函数y=
如图,?OABC的顶点O在坐标原点,顶点A、C在反比例函数y= 如图,AB为⊙O的直径,C为AE的中点,连结AE交BC于F点.
如图,AB为⊙O的直径,C为AE的中点,连结AE交BC于F点.