题目内容
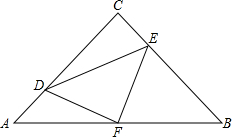 如图,在Rt△ABC中,AC=BC,∠C=90°,AB=8,点F是AB边的中点,点D、E分别在AC、BC边上运动,且保持AD=CE,连接DE、DF、EF.在此运动变化的过程中,下列结论中正确的结论是
如图,在Rt△ABC中,AC=BC,∠C=90°,AB=8,点F是AB边的中点,点D、E分别在AC、BC边上运动,且保持AD=CE,连接DE、DF、EF.在此运动变化的过程中,下列结论中正确的结论是①△DFE是等腰直角三角形;
②四边形CDFE不可能为正方形;
③DE长度的最小值是4;
④四边形CDFE的面积保持不变;
⑤△CDE面积的最大值为4.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:如图,作辅助线;证明△ADF≌△CEF,进而得到DF=EF,四边形DCEF的面积=16,故①④正确;证明当FD⊥AC时,FD最小=4,四边形DCEF为正方形,同时△DCE的面积最大=8,故③正确,②⑤错误.
解答: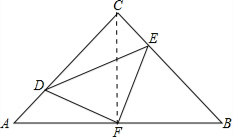 解:如图,连接CF;
解:如图,连接CF;
∵△ABC为等腰直角三角形,且点F为AB的中点,
∴∠A=45°,∠FCB=45°,AF=CF;
在△ADF与△CEF中,
,
∴△ADF≌△CEF(SAS),
∴DF=EF,S△ADF=S△CEF,
∴S四边形DCEF=S△ACF=
S△ABC=
×
×8×8=16,
故①④正确;
当FD⊥AC时,DF最小,此时,
∵∠DCE=∠CDF=∠CEF,且DF=EF,
∴四边形DCEF为正方形,
故②错误;
当FD⊥AC时,∵CF=AF,
∴AD=CD=4,故③正确;
∵四边形DCEF的面积为定值,
∴当△DEF的面积最小时,△DCE的面积最大,
而△DEF的面积最小值=
×4×4=8,
∴△DCE的面积最大值=16-8=8,
故⑤错误,
∴综上所述,正确结论是:①③④.
答案为①③④.
 解:如图,连接CF;
解:如图,连接CF;∵△ABC为等腰直角三角形,且点F为AB的中点,
∴∠A=45°,∠FCB=45°,AF=CF;
在△ADF与△CEF中,
|
∴△ADF≌△CEF(SAS),
∴DF=EF,S△ADF=S△CEF,
∴S四边形DCEF=S△ACF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故①④正确;
当FD⊥AC时,DF最小,此时,
∵∠DCE=∠CDF=∠CEF,且DF=EF,
∴四边形DCEF为正方形,
故②错误;
当FD⊥AC时,∵CF=AF,
∴AD=CD=4,故③正确;
∵四边形DCEF的面积为定值,
∴当△DEF的面积最小时,△DCE的面积最大,
而△DEF的面积最小值=
| 1 |
| 2 |
∴△DCE的面积最大值=16-8=8,
故⑤错误,
∴综上所述,正确结论是:①③④.
答案为①③④.
点评:该题主要考查了全等三角形的判定、正方形的判定、等腰直角三角形的性质等几何知识点及其应用问题;解题的关键是牢固掌握全等三角形的判定、正方形的判定、等腰直角三角形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,将一副三角尺按不同位置摆放,在哪种摆放方式中∠α与∠β互余?在哪种摆放方式中∠α与∠β互补?在哪种摆放方式中∠α与∠β相等?
如图,将一副三角尺按不同位置摆放,在哪种摆放方式中∠α与∠β互余?在哪种摆放方式中∠α与∠β互补?在哪种摆放方式中∠α与∠β相等?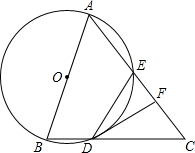 如图,已知AB=AC,以AB为直径的⊙O分别交BC,AC于D,E两点,F为CE的中点,连接DF,DE.
如图,已知AB=AC,以AB为直径的⊙O分别交BC,AC于D,E两点,F为CE的中点,连接DF,DE. 已知 四边形ABCD中,∠ABD=∠CBD=∠ACD=30°,BE=4,DE=2,则S△ABC=
已知 四边形ABCD中,∠ABD=∠CBD=∠ACD=30°,BE=4,DE=2,则S△ABC=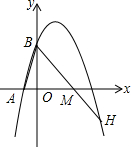 抛物线y=-
抛物线y=- 如图所示:在△ABC中,AD为BC边上的中线,AC=
如图所示:在△ABC中,AD为BC边上的中线,AC=