题目内容
7.若x1,x2是关于x的一元二次方程x2+(k+3)x+2=0的两个根,已知x1=-2,则|x1-x2|的值为1.分析 将x1=-2代入原方程可得出关于k的一元一次方程,解方程即可求出k值,再将k值代入原方程,根据根与系数的关系找出“x1+x2=-3,x1•x2=2”,将|x1-x2|变形为$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}•{x}_{2}}$,套入数据即可得出结论.
解答 解:∵x=-2是方程x2+(k+3)x+2=0的根,
∴4-2(k+3)+2=0,
解得:k=0.
∴原方程为x2+3x+2=0.
∵x1,x2是关于x的一元二次方程x2+(k+3)x+2=0的两个根,
∴x1+x2=-3,x1•x2=2,
∴|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}•{x}_{2}}$=$\sqrt{(-3)^{2}-4×2}$=1.
故答案为:1.
点评 本题考查了根与系数的关系、解一元一次方程以及完全平方公式,解题的关键是找出“x1+x2=-3,x1•x2=2”.本题属于基础题,难度不大,解决该题型题目时,由根与系数的关系找出两根之和与两根之积,再利用完全平方公式将|x1-x2|转化成只含两根之和与两根之积的形式是关键.

练习册系列答案
相关题目
2.要使分式$\frac{-5}{x-1}$有意义,则x的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x<1 | D. | x≠-1 |
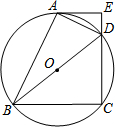 如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE. 如图,在平面直角坐标系xOy中,点m在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C,D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-2,0),AE=8,
如图,在平面直角坐标系xOy中,点m在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C,D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-2,0),AE=8, 据每日邮报报道,按照美国创业家伊隆•马斯克(Elon Musk)最近提出的“超级高铁”(Hyperloop)的设计,超级高铁的速度在理想状态下最高可以达到时速6500公里,预计从北京到纽约仅需2小时,但造价极高,每8公里造价高达620000000美元,数据620000000用科学记数法表示为( )
据每日邮报报道,按照美国创业家伊隆•马斯克(Elon Musk)最近提出的“超级高铁”(Hyperloop)的设计,超级高铁的速度在理想状态下最高可以达到时速6500公里,预计从北京到纽约仅需2小时,但造价极高,每8公里造价高达620000000美元,数据620000000用科学记数法表示为( )
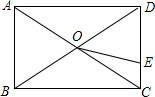 如图,矩形ABCD,对角线AC,BD相交于点O,点E是边CD上一动点,已知AC=10,CD=6,则OE的最小值是4.
如图,矩形ABCD,对角线AC,BD相交于点O,点E是边CD上一动点,已知AC=10,CD=6,则OE的最小值是4.