题目内容
16.探究:如图①,在△ABC外作△BAD,△CAE,使∠BAD=∠CAE=90°,AB=AD,AC=AE,以AD,AE为邻边向上作平行四边形ADFE,连接AF,求证:△ADF≌△BAC;应用:如图②,在图①的基础上,取BD的中点P,连接PF,PC,PA,求∠FPC的度数,并说明理由.

分析 探究:由四边形AEFD是平行四边形,得到DF=AE,∠ADF+∠DAE=180°,等量代换得到DF=AC,∠ADF=∠BAC,根据全等三角形的判定定理即可得到结论.
应用:由四边形AEFD是平行四边形,得到DF=AE=AC,DF∥AE,根据平行线的性质得到∠BAC=∠ADF,证得∠PDF=∠PAC,
根据全等三角形的性质得到PF=PC,∠DPF=∠APC,即可得到结论.
解答 证明:探究:∵四边形AEFD是平行四边形,
∴DF=AE,∠ADF+∠DAE=180°,
∵AC=AE,
∴DF=AC,
∵∠BAD=∠CAE=90°,
∴∠BAC+∠DAE=180°,
∴∠ADF=∠BAC,
在△ABC与△ADF中,$\left\{\begin{array}{l}{AB=AD}\\{∠BAC=∠ADF}\\{AC=DF}\end{array}\right.$,
∴△ABC≌△ADF;
应用:∵AB=AD,∠BAD=90°,PD=PB,
∴PA=PD=PB,∠ADB=∠ABD=∠PAD=45°,PA⊥BD,
∴∠DPA=90°
∵四边形AEFD是平行四边形,
∴DF=AE=AC,DF∥AE,
∴∠DAE+∠ADF=180°
∵∠BAD=∠CAE=90°,
∴∠BAC+∠DAE=180°,
∴∠BAC=∠ADF,
∵∠PDF=∠ADB+∠ADF=45°+∠ADF,
∠PAC=∠PAB+∠BAC=45°+∠BAC,
∴∠PDF=∠PAC,
在△PDF和△PAC中,
$\left\{\begin{array}{l}{PD=PA}\\{∠PDF=∠PAC}\\{DF=AC}\end{array}\right.$,
∴△PDF≌△PAC,
∴PF=PC,∠DPF=∠APC,
∴∠DPA=∠FPC=90°.
点评 本题考查全等三角形的判定和性质、平行四边形的性质,等腰直角三角形的性质,熟记掌握全等三角形的判定和性质是解题的关键.

| A. | 1-(1-x)=1 | B. | 1+(1-x)=1 | C. | 1-(1-x)=x-2 | D. | 1+(1-x)=x-2 |
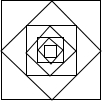 如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形四边中点为顶点作四边形,…依次作下去,图中所作的第n个四边形的周长为$4{(\frac{{\sqrt{2}}}{2})^n}$.
如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形四边中点为顶点作四边形,…依次作下去,图中所作的第n个四边形的周长为$4{(\frac{{\sqrt{2}}}{2})^n}$.
 将含有30°角的直角三角板的直角顶点放在平行的两条直线的一条直线上,若∠2=23°,则∠1的度数是37°.
将含有30°角的直角三角板的直角顶点放在平行的两条直线的一条直线上,若∠2=23°,则∠1的度数是37°.