题目内容
17.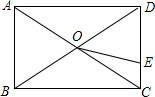 如图,矩形ABCD,对角线AC,BD相交于点O,点E是边CD上一动点,已知AC=10,CD=6,则OE的最小值是4.
如图,矩形ABCD,对角线AC,BD相交于点O,点E是边CD上一动点,已知AC=10,CD=6,则OE的最小值是4.
分析 先由勾股定理求出BC=8,再证明OE是△BCD的中位线,再根据三角形的中位线等于第三边的一半求解即可.
解答 解:∵四边形ABCD是矩形,
∴BD=AC=10,∠BCD=90°,
∴BC=$\sqrt{B{D}^{2}-C{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
当OE⊥CD时,OE最小,
此时OE∥BC,
∵OB=OD,
∴OE是△BCD的中位线,
∴OE=$\frac{1}{2}$BC=4;
故答案为:4.
点评 本题考查了矩形的性质和三角形的中位线定理、勾股定理;熟练掌握矩形的性质,证出OE是三角形的中位线是解决问题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
2.下列各整式中,次数为3次的单项式是( )
| A. | xy2 | B. | xy3 | C. | x+y2 | D. | x+y3 |

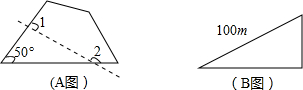 请从以下两题中任选一题作答,若多选,则按所选的第一题计分.
请从以下两题中任选一题作答,若多选,则按所选的第一题计分.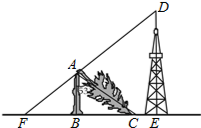 如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33) 将含有30°角的直角三角板的直角顶点放在平行的两条直线的一条直线上,若∠2=23°,则∠1的度数是37°.
将含有30°角的直角三角板的直角顶点放在平行的两条直线的一条直线上,若∠2=23°,则∠1的度数是37°.