题目内容
19.已知m、n是关于x的一元二次方程x2-2x-1=0的两个实数根,则代数式3m2-n2-8m+1的值等于-1.分析 根据根与系数的关系得出“m+n=2,mn=-1”,再将3m2-n2-8m+1变形为只含m+n与mn的代数式,代入数据即可得出结论.
解答 解:∵m、n是关于x的一元二次方程x2-2x-1=0的两个实数根,
∴m+n=-$\frac{b}{a}$=2,mn=$\frac{c}{a}$=-1.
∴3m2-n2-8m+1=(4m2-8m)-(m2+n2)+1=-4mn-[(m+n)2-2mn]+1=4-6+1=-1.
故答案为:-1.
点评 本题考查了根与系数的关系,解题的关键是找出3m2-n2-8m+1=-4mn-[(m+n)2-2mn]+1.本题属于基础题,难度不大,解决该题型题目时,根据根与系数的关系找出两根之和与两根之积,再将代数式变形为只含两根之和与两根之积的形式是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.把分式方程$\frac{1}{x-2}$-$\frac{1-x}{2-x}$=1化为整式方程正确的是( )
| A. | 1-(1-x)=1 | B. | 1+(1-x)=1 | C. | 1-(1-x)=x-2 | D. | 1+(1-x)=x-2 |
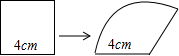 手工课上,小明将一个边长为4cm的正方形铁丝框,变形成为如图所示一个扇形框,周长不变,且扇形框半径等于正方形的边长,则该扇形的面积大小为16cm2.
手工课上,小明将一个边长为4cm的正方形铁丝框,变形成为如图所示一个扇形框,周长不变,且扇形框半径等于正方形的边长,则该扇形的面积大小为16cm2.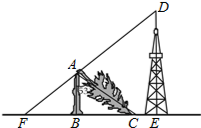 如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)