题目内容
15. 如图,在平面直角坐标系xOy中,点m在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C,D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-2,0),AE=8,
如图,在平面直角坐标系xOy中,点m在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C,D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-2,0),AE=8,(1)求证:AE=CD;
(2)求点C坐标和⊙M直径AB的长;
(3)求OG的长.
分析 (1)要证明AE=CD,即证明$\widehat{ACE}=\widehat{CAD}$,由点C是$\widehat{AE}$的中点和AB⊥CD可知,$\widehat{AD}=\widehat{AC}=\widehat{CE}$,从而可得$\widehat{ACE}=\widehat{CAD}$;
(2)由垂径定理可知:OC=$\frac{1}{2}$CD=$\frac{1}{2}$AE=4,所以点C的坐标为(0,4),连接AC和BC后,证明△CAO∽△BAC,可得CA2=AO•AB,从而可求出AB的长度;
(3)由$\widehat{CE}=\widehat{AD}$可知,AG=CG,设AG=x,则OG=4-x,利用勾股定理可列出方程即可求出x的值.
解答 解:(1)∵点C是$\widehat{AE}$的中点,
∴$\widehat{AC}=\widehat{CE}$,
∵AB⊥CD,
∴由垂径定理可知:$\widehat{AC}$=$\widehat{AD}$,
∴$\widehat{AC}=\widehat{CE}=\widehat{AD}$,
∴$\widehat{ACE}=\widehat{CAD}$,
∴AE=CD;
(2)连接AC、BC,
由(1)可知:CD=AE=8,
∴由垂径定理可知:OC=$\frac{1}{2}$CD=4,
∴C的坐标为(0,4),
由勾股定理可求得:CA2=22+42=20,
∵AB是⊙M的直径,
∴∠ACB=90°,
∵∠CAB=∠CAB,
∴△CAO∽△BAC,
∴$\frac{CA}{AO}=\frac{AB}{CA}$,
∴CA2=AO•AB,
∴AB=$\frac{20}{2}$=10;
(3)由(1)可知:$\widehat{CE}=\widehat{AD}$,
∴∠ACD=∠CAE,
∴AG=CG,
设AG=x,
∴CG=x,OG=OC-CG=4-x,
∴由勾股定理可求得:AO2+OG2=AG2,
∴22+(4-x)2=x2,
∴x=$\frac{5}{2}$,
∴OG=4-x=$\frac{3}{2}$
点评 本题考查圆的综合问题,涉及垂径定理,勾股定理,相似三角形的判定和性质等知识,综合程度较高,需要学生灵活运用所学知识进行解答.

 应用题作业本系列答案
应用题作业本系列答案 尺规作图:已知△ABC,如图.
尺规作图:已知△ABC,如图.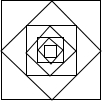 如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形四边中点为顶点作四边形,…依次作下去,图中所作的第n个四边形的周长为$4{(\frac{{\sqrt{2}}}{2})^n}$.
如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形四边中点为顶点作四边形,…依次作下去,图中所作的第n个四边形的周长为$4{(\frac{{\sqrt{2}}}{2})^n}$.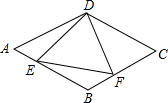 如图,在菱形ABCD中,AB=6,∠A=60°,点E、F分别在AB,BC上,且AE=BF,下列结论中:
如图,在菱形ABCD中,AB=6,∠A=60°,点E、F分别在AB,BC上,且AE=BF,下列结论中: