题目内容
1．
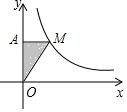如图，M为反比例函数y=$\frac{k}{x}$图象上一点，MA⊥y轴于点A，S△MAO=2时，k=4．
分析 根据直角三角形的面积公式可得AM•AO=4，再根据反比例函数图象上点的坐标特点可得k的值．
解答 解：如图所示：∵MA⊥y轴于点A，S△MAO=2，
∴AM•AO=4，
∴k=4．
故答案为：4．
点评 此题主要考查了反比例函数图象上点的坐标特点，在反比例函数y=$\frac{k}{x}$图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．
练习册系列答案
相关题目
如图，计算∠A+∠B+∠C+∠D+∠E的度数．
如图，点O为直线AB上一点，过点O作射线OC，已知∠AOC不是直角，射线OD平分∠AOC，射线OE平分∠BOC，射线OF平分∠DOE．
已知线段AB，延长线段AB至C点，使点B为AC的中点，反向延长线段AB至D点，使AD=$\frac{1}{2}$AB．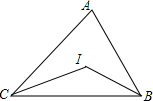
如图，在△ABC中，∠ABC、∠ACB的平分线相交于点I，根据下列条件，求∠BIC的度数．
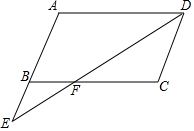如图，在?ABCD中，点E是AB延长线上一点，连结DE与BC相交于点F，且$\frac{BF}{FC}$=$\frac{1}{2}$．