题目内容
5．
如图，计算∠A+∠B+∠C+∠D+∠E的度数．
分析 连接AC，根据三角形的内角和定理求出∠D+∠E=∠OAC+∠OCA，再利用三角形的内角和等于180°求解即可．
解答 
解：如图，连接AC，
∵∠D+∠E+∠DOE=180°，
∠OAC+∠OCA+∠AOC=180°，
∠DOE=∠AOC（对顶角相等），
∴∠D+∠E=∠OAC+∠OCA，
在△ABC中，∠BAC+∠B+∠ACB=180°，
所以，∠BAO+∠CAO+∠B+∠BCO+∠ACO=180°，
所以，∠A+∠B+∠C+∠D+∠E=180°．
点评 本题考查了三角形的内角和定理，熟记定理并准确识图理清图中各角度之间的关系是解题的关键．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
已知某四棱柱的俯视图如图所示，画出它的主视图和左视图．
如图所示，C，D是线段AB上的两点，AC=$\frac{5}{9}$BC，AD=$\frac{9}{5}$DB，若CD=2cm，求线段AB的长．
20．在外打工的小王，利用打工赚来的积蓄，准备在家乡创办小型零部件加工企业，该零部件按规格分为5种型号，据调研显示，每种型号的日产量见下表所列（每种型号的产品每天都能销售完）．
由于刚创办，该企业只能生产一种型号的产品．
（1）求y与x的函数关系式．
（2）已知销售单价z元与型号x之间满足x=10x+60，小王为了扩大日销售额，应选择生产那种型号的零件？并求出当日销售额ρ的最大值．
（3）若生产每种型号产品的每件成本q元与x满足关系：q=4x+36，且日销售额不大于7000元时，需缴纳销售额5%的税收，且销售额超过7000元的需缴纳销售额10%的税收，小王生产哪一种型号可使每日获得的利润最高？
注：日销售额=日产量×销售单价；每日利润=日产量×（产品单价-成本）-税收．
| 产品型号x | 1 | 2 | 3 | 4 | 5 |
| 日产量y（件） | 100 | 90 | 80 | 70 | 60 |
（1）求y与x的函数关系式．
（2）已知销售单价z元与型号x之间满足x=10x+60，小王为了扩大日销售额，应选择生产那种型号的零件？并求出当日销售额ρ的最大值．
（3）若生产每种型号产品的每件成本q元与x满足关系：q=4x+36，且日销售额不大于7000元时，需缴纳销售额5%的税收，且销售额超过7000元的需缴纳销售额10%的税收，小王生产哪一种型号可使每日获得的利润最高？
注：日销售额=日产量×销售单价；每日利润=日产量×（产品单价-成本）-税收．
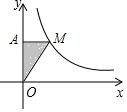如图，M为反比例函数y=$\frac{k}{x}$图象上一点，MA⊥y轴于点A，S△MAO=2时，k=4．