题目内容
10.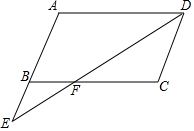 如图,在?ABCD中,点E是AB延长线上一点,连结DE与BC相交于点F,且$\frac{BF}{FC}$=$\frac{1}{2}$.
如图,在?ABCD中,点E是AB延长线上一点,连结DE与BC相交于点F,且$\frac{BF}{FC}$=$\frac{1}{2}$.(1)求$\frac{BE}{AE}$的值.
(2)若△BEF的面积是1,求?ABCD的面积.
分析 (1)根据三角形相似和平行四边形的性质可以得到$\frac{BE}{AE}$的值;
(2)要求?ABCD的面积,只要求出CF与BC的比值即可,然后根据三角形相似和平行四边形的性质可以得到?ABCD的面积.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴△BFE∽△CFD,
∴$\frac{BE}{CD}=\frac{BF}{FC}$,
∵$\frac{BF}{FC}$=$\frac{1}{2}$,
∴$\frac{BE}{CD}=\frac{1}{2}$,
∴$\frac{BE}{AE}=\frac{1}{3}$;
(2))∵四边形ABCD是平行四边形,$\frac{BF}{FC}$=$\frac{1}{2}$,
∴AB∥CD,AB=CD,
∴△BFE∽△CFD,
∴$\frac{{S}_{△BFE}}{{S}_{△CFD}}=(\frac{1}{2})^{2}=\frac{1}{4}$,
∵△BEF的面积是1,
∴△CDF的面积是4,
∵$\frac{CF}{CB}=\frac{2}{3}$,
∴$\frac{{S}_{△CFD}}{{S}_{平行四边形ABCD}}=\frac{CF}{BC}$=$\frac{2}{3}$,
∴?ABCD的面积是6.
点评 本题考查平行四边形的性质和相似三角形的性质和判定,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
20.火车票上的车次号有两个意义:一是数字越小表示车速越快,1-98次为特快列车,101-198次为直快列车,301-398次为普快列车,401-498次为普客列车;二是单数与双数表示不同的行驶方向,其中单数表示从南京开出,双数表示开往南京.根据以上信息,上海开往南京的某一直快列车的车次号可能是( )
| A. | 20 | B. | 119 | C. | 120 | D. | 319 |
5.滕州市某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
经统计发现两班总数相等,此时有学生建议,可以通过考察数据中的其他信息作为参考,请你回答下列问题:
(1)分别求出两班5名学生比赛成绩的中位数;
(2)计算并比较两班比赛数据的方差哪个小?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
(1)分别求出两班5名学生比赛成绩的中位数;
(2)计算并比较两班比赛数据的方差哪个小?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
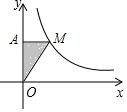 如图,M为反比例函数y=$\frac{k}{x}$图象上一点,MA⊥y轴于点A,S△MAO=2时,k=4.
如图,M为反比例函数y=$\frac{k}{x}$图象上一点,MA⊥y轴于点A,S△MAO=2时,k=4. 如图,已知⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8,.过点B作⊙O的切线BD,过点A作AD⊥BD,垂足为D.
如图,已知⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8,.过点B作⊙O的切线BD,过点A作AD⊥BD,垂足为D.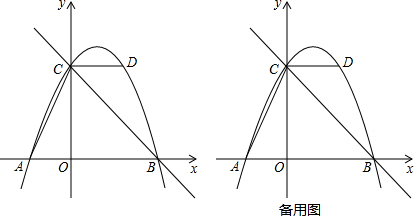
 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B,连结BC.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B,连结BC.