题目内容
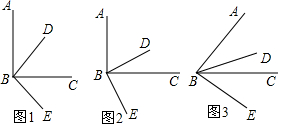
16.已知∠ABC=∠DBE,射线BD在∠ABC的内部,按要求完成下列各小题.尝试探究:如图1,已知∠ABC=90°,当BD是∠ABC的平分线时,∠ABE+∠DBC的度数为180°;
初步应用:如图2,已知∠ABC=90°,若BD不是∠ABC的平分线,求∠ABE+∠DBC的度数;
拓展提升:如图3,若∠ABC=45°时,试判断∠ABE与∠DBC之间的数量关系,并说明理由.
分析 尝试探究:利用角平分线的性质,先求出∠DBC、∠CBE的度数,再计算∠ABE+∠DBC的度数;
初步应用:利用角的和差关系,把∠ABE+∠DBC转化为∠ABC+∠DBE,代入已知得出结论;
拓展提升:同初步探究,把∠ABE+∠DBC转化为∠ABC+∠DBE,代入计算得出结论.
解答  解:尝试探究:∵∠ABC=90°,BD平分∠ABC,
解:尝试探究:∵∠ABC=90°,BD平分∠ABC,
所以∠DBC=45°,
因为∠DBE=∠ABC=90°,∠DBC+∠CBE=∠DBE
所以∠CBE=45°.
所以∠ABE+∠DBC=∠ABC+∠CBE+∠DBC=90°+45°+45°=180°.
初步应用:因为∠DBE=∠ABC=90°,
所以∠ABE+∠DBC=∠ABC+∠CBE+∠DBC
=∠ABC+∠DBE=180°.
答:∠ABE+∠DBC的度数为180°.
拓展提升:∠ABE+∠DBC=90°.
理由:
因为∠DBE=∠ABC=45°,
所以∠ABE+∠DBC=∠ABC+∠CBE+∠DBC
=∠ABC+∠DBE=90°.
点评 本题考查了角的和差关系及角的相关计算.通过观察图形,把∠ABE+∠DBC转化为∠ABC+∠DBE是解决本题的关键.

练习册系列答案
相关题目
20.在外打工的小王,利用打工赚来的积蓄,准备在家乡创办小型零部件加工企业,该零部件按规格分为5种型号,据调研显示,每种型号的日产量见下表所列(每种型号的产品每天都能销售完).
由于刚创办,该企业只能生产一种型号的产品.
(1)求y与x的函数关系式.
(2)已知销售单价z元与型号x之间满足x=10x+60,小王为了扩大日销售额,应选择生产那种型号的零件?并求出当日销售额ρ的最大值.
(3)若生产每种型号产品的每件成本q元与x满足关系:q=4x+36,且日销售额不大于7000元时,需缴纳销售额5%的税收,且销售额超过7000元的需缴纳销售额10%的税收,小王生产哪一种型号可使每日获得的利润最高?
注:日销售额=日产量×销售单价;每日利润=日产量×(产品单价-成本)-税收.
| 产品型号x | 1 | 2 | 3 | 4 | 5 |
| 日产量y(件) | 100 | 90 | 80 | 70 | 60 |
(1)求y与x的函数关系式.
(2)已知销售单价z元与型号x之间满足x=10x+60,小王为了扩大日销售额,应选择生产那种型号的零件?并求出当日销售额ρ的最大值.
(3)若生产每种型号产品的每件成本q元与x满足关系:q=4x+36,且日销售额不大于7000元时,需缴纳销售额5%的税收,且销售额超过7000元的需缴纳销售额10%的税收,小王生产哪一种型号可使每日获得的利润最高?
注:日销售额=日产量×销售单价;每日利润=日产量×(产品单价-成本)-税收.
7.蜗牛从树根沿着树干往上爬,白天爬上4米,夜间滑下3米,那么高7米的树,蜗牛爬到树顶要( )
| A. | 3天 | B. | 4天 | C. | 5天 | D. | 6天 |
5.滕州市某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
经统计发现两班总数相等,此时有学生建议,可以通过考察数据中的其他信息作为参考,请你回答下列问题:
(1)分别求出两班5名学生比赛成绩的中位数;
(2)计算并比较两班比赛数据的方差哪个小?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
(1)分别求出两班5名学生比赛成绩的中位数;
(2)计算并比较两班比赛数据的方差哪个小?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
 已知:如图,AB平分∠CAD,∠C=∠D.求证:CB=DB.
已知:如图,AB平分∠CAD,∠C=∠D.求证:CB=DB.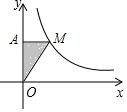 如图,M为反比例函数y=$\frac{k}{x}$图象上一点,MA⊥y轴于点A,S△MAO=2时,k=4.
如图,M为反比例函数y=$\frac{k}{x}$图象上一点,MA⊥y轴于点A,S△MAO=2时,k=4. 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.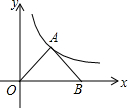 已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.
已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.