题目内容
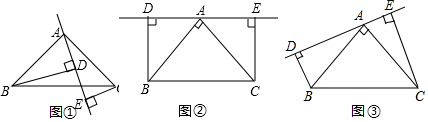
11.如图①,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD⊥AE于D,CE⊥AE于E.(1)求证:BD=DE+CE.
(2)若直线AE旋转到图②与图③位置时,判断BD与DE,CE的关系,并说明理由.
分析 (1)在直角三角形中,由题中条件可得∠ABD=EAC,又有AB=AC,则有一个角及斜边相等,则可判定Rt△BAD≌Rt△AEC,由三角形全等可得三角形对应边相等,进而通过线段之间的转化,可得出结论;
(2)由题中条件同样可得出Rt△BAD≌Rt△AEC,得出对应线段相等,进而可得线段之间的关系.
解答 (1)证明:∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠ABD+∠BAD=90°,∠BAD+∠EAC=90,
∴∠ABD=∠EAC.
在Rt△BDA和Rt△AEC中,
∵$\left\{\begin{array}{l}{∠ABD=∠EAC}\\{∠ADB=∠AEC=90°}\\{AB=AC}\end{array}\right.$,
∴Rt△BAD≌Rt△AEC(AAS),
∴BD=AE,AD=CE,BD=AE,
∴BD=AE=AD+DE=CE+DE;
(2)解:BD=DE-CE.
理由:∵∠BAC=90°,BD⊥AE,CE⊥AE
∴∠ABD+∠BAD=90°,∠BAD+∠EAC=90°,
∴∠ABD=∠EAC,
在Rt△BDA和Rt△AEC中,
∵$\left\{\begin{array}{l}{∠ABD=∠EAC}\\{∠ADB=∠CEA}\\{AB=AC}\end{array}\right.$,
∴Rt△BAD≌Rt△AEC(AAS),
∴BD=AE,AD=CE,
∴BD=AE=DE-AD=DE-CE.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
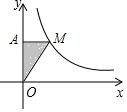 如图,M为反比例函数y=$\frac{k}{x}$图象上一点,MA⊥y轴于点A,S△MAO=2时,k=4.
如图,M为反比例函数y=$\frac{k}{x}$图象上一点,MA⊥y轴于点A,S△MAO=2时,k=4.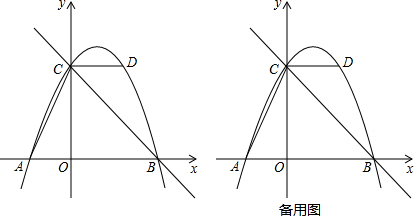
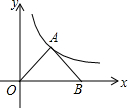 已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.
已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.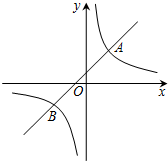 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点.
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点.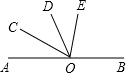 如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,求∠BOE的度数.
如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,求∠BOE的度数. 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B,连结BC.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B,连结BC.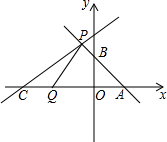 如图,直线l1:y1=-x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2=$\frac{1}{2}$x+b过点P,与x轴交于点C.
如图,直线l1:y1=-x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2=$\frac{1}{2}$x+b过点P,与x轴交于点C.