题目内容
4．解方程：2$\sqrt{{x}^{2}-2x+4}$=3x2-6x+4．分析 本题含根号，计算比较不便，因此可先把x2-2x=y，再方程两边平方，然后对方程进行因式分解即可解出本题．
解答 解：设x2-2x=y，原方程可化为：$2\sqrt{y+4}=3y+4$，
两边平方可得：4（y+4）=9y2+24y+16，
可得：y（9y+20）=0，
∴y=0或y=-$\frac{20}{9}$
∵y=-$\frac{20}{9}$时不满足题意．
∴y=0
∴x2-2x=0
∴x=0或x=2．
检验，把x=0代入原方程后，等式右边=左边，是原方程的解；
把x=2代入原方程后，等式右边=左边，是原方程的解．
点评 本题考查了一元二次方程的解法．解一元二次方程常用的方法有直接开平方法，配方法，公式法，因式分解法，要根据方程的提点灵活选用合适的方法．本题运用的是因式分解法和平方法．
练习册系列答案
相关题目
15．在?ABCD中，BC边上的高为AE=4，AB=5，EC=2，则?ABCD的周长等于（ ）
| A． | 12 | B． | 16 | C． | 16或24 | D． | 20 |
19．已知关于x的方程（x-a）（x-b）-1=0（a＜b）的两根为p、q（p＜q，且pq＞0），则一定有（ ）
| A． | a＜p＜q＜b | B． | $\frac{q}{p}$＞$\frac{b}{a}$ | C． | $\frac{1}{q}$＜$\frac{1}{b}$＜$\frac{1}{a}$＜$\frac{1}{p}$ | D． | $\frac{1}{a}$＜$\frac{1}{p}$＜$\frac{1}{q}$＜$\frac{1}{b}$ |
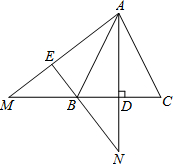如图，在△ABC中，AB=AC，AD⊥BC于D点，把△ACD绕着A点顺时针旋转，使得AC与AB重合，点D落在点E处，延长AE、CB相交于M点，延长EB、AD相交于N点．求证：AM=AN．
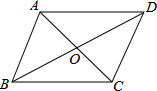如图，平行四边形ABCD的对角线相交于点O，请你添加一个条件AC=BD．答案不唯一．．（只添一个即可），使平行四边形ABCD是矩形．