题目内容
19.已知关于x的方程(x-a)(x-b)-1=0(a<b)的两根为p、q(p<q,且pq>0),则一定有( )| A. | a<p<q<b | B. | $\frac{q}{p}$>$\frac{b}{a}$ | C. | $\frac{1}{q}$<$\frac{1}{b}$<$\frac{1}{a}$<$\frac{1}{p}$ | D. | $\frac{1}{a}$<$\frac{1}{p}$<$\frac{1}{q}$<$\frac{1}{b}$ |
分析 首先把方程化为一般形式,由于p、q是方程的解,根据根与系数的关系即可得到a,b,p、q之间的关系,然后对四者之间的大小关系进行讨论即可判断.
解答 解:设y=(x-a)(x-b),
则此二次函数开口向上,
当(x-a)(x-b)=0时,
即函数与x轴的交点为:(a,0),(b,0),
当(x-a)(x-b)=1时,
∵p、q是关于x的方程(x-a)(x-b)-1=0的两实根,
∴函数与y=1的交点为:(p,1),(q,1),
根据二次函数的增减性,可得:
当a<b,p<q时,p<a<b<q,
∴$\frac{q}{p}$>$\frac{b}{a}$,
故选:B.
点评 此题主要考查了一元二次方程根的分布,根据题意得出p<a<b<q是解题关键.

练习册系列答案
相关题目
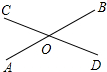 如图,直线AB与CD相交于点O,∠AOC:∠COB=2:3,则∠BOD=72°.
如图,直线AB与CD相交于点O,∠AOC:∠COB=2:3,则∠BOD=72°.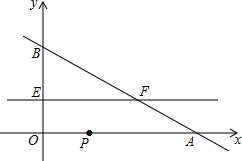 如图,在平面直角坐标系中,直线y=-0.5x+2与坐标轴分别交于A,B两点,动点P从A点出发沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为2,1,$\sqrt{5}$(长度单位/秒),点E同时从O点出发沿OB以$\frac{1}{3}$(长度单位/秒)的速度运动,直线EF∥x轴交BA于点F,设运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,点P和点E同时停止运动,请解答下列问题:
如图,在平面直角坐标系中,直线y=-0.5x+2与坐标轴分别交于A,B两点,动点P从A点出发沿折线AO-OB-BA运动,点P在AO,OB,BA上运动的速度分别为2,1,$\sqrt{5}$(长度单位/秒),点E同时从O点出发沿OB以$\frac{1}{3}$(长度单位/秒)的速度运动,直线EF∥x轴交BA于点F,设运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,点P和点E同时停止运动,请解答下列问题: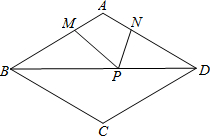 如图,在菱形ABCD中,AB=6,∠ABC=60°,点M、N分别在AB、AD边上,AM=AN=2,P是对角线BD上的动点,则PM+PN的最小值是2$\sqrt{7}$.
如图,在菱形ABCD中,AB=6,∠ABC=60°,点M、N分别在AB、AD边上,AM=AN=2,P是对角线BD上的动点,则PM+PN的最小值是2$\sqrt{7}$.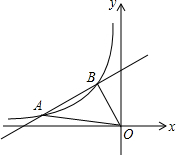 如图,已知一次函数y=$\frac{1}{2}$x+b与反比例函数y=$\frac{m}{x}$在第二象限的图象交于A(n,$\frac{1}{2}$)、B(-1,2)两点.
如图,已知一次函数y=$\frac{1}{2}$x+b与反比例函数y=$\frac{m}{x}$在第二象限的图象交于A(n,$\frac{1}{2}$)、B(-1,2)两点.