题目内容
14．某汽车销售公司经销某品牌A款汽车，随着汽车的普及，其价格也在不断下降．今年5月份A款汽车的售价比去年同期每辆降价1万元，如果卖出相同数量的A款汽车，去年销售额为100万元，今年销售额只有90万元．（1）今年5月份A款汽车每辆售价多少万元？
（2）为了增加收入，汽车销售公司决定再经销同品牌的B款汽车，已知A款汽车每辆进价为7.5万元，B款汽车每辆进价为6万元，公司预计用不多于105万元的资金购进这两款汽车共15辆，问A款汽车最多能购进多少辆？
分析 （1）设今年5月份A款汽车每辆售价x万元，根据题意可得，去年销售额100万元与今年销售额90万元所卖的车辆数量相等，据此列方程求解；
（2）设A款汽车能购进y辆，则B款汽车能购进（15-y）辆，根据购车资金不多于105万元，列不等式求解．
解答 解：（1）设今年5月份A款汽车每辆售价x万元，则去年同期每辆售价（x+1）万元，
由题意得，$\frac{100}{x+1}$=$\frac{90}{x}$，
解得：x=9，
经检验：x=9是原分式方程的解，且符合题意，
答：今年5月份A款汽车每辆售价9万元；
（2）设A款汽车能购进y辆，则B款汽车能购进（15-y）辆，
由题意得，7.5y+6（15-y）≤105，
解得：y≤10．
答：A款汽车最多能购进10辆．
点评 本题考查了分式方程和一元一次不等式的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程和不等式求解．
练习册系列答案
相关题目
19．直线y=$\frac{1}{2}$x和直线y=-x+3所夹锐角为α，则sinα的值为（ ）
| A． | $\frac{3\sqrt{10}}{10}$ | B． | $\frac{\sqrt{10}}{10}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
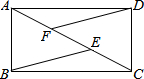如图所示，E，F是矩形ABCD对角线AC上的两点，试添加一个条件：AF=CE，使得BE∥DF．
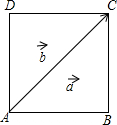如图，在正方形ABCD中，如果AC=3$\sqrt{2}$，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，那么|$\overrightarrow{a}$-$\overrightarrow{b}$|=3．