题目内容
1．求证：不论a取何值，a2-a+1的值总是一个正数．分析 直接利用完全平方公式将原式变形，再利用偶次方的性质得出答案．
解答 证明：∵a2-a+1=（a-$\frac{1}{2}$）2+$\frac{3}{4}$，
（a-$\frac{1}{2}$）2≥0，
∴（a-$\frac{1}{2}$）2+$\frac{3}{4}$＞0，
∴不论a取何值，a2-a+1的值总是一个正数．
点评 此题主要考查了配方法的应用，正确应用完全平方公式是解题关键．
练习册系列答案
53随堂测系列答案
相关题目
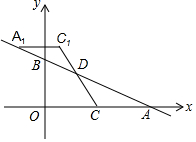如图，一次函数y=-$\frac{1}{2}$x+m（m＞0）的图象与x轴、y轴分别交于点A、B，点C在线段OA上，点C的横坐标为n，点D在线段AB上，AD=2BD，将△ACD绕点D旋转180°后得到△A1C1D．
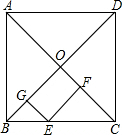如图，在正方形ABCD中，E为BC上任意一点，EF⊥AC于F，EG⊥BD于F，试说明：EF+EG=OB．
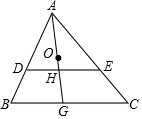如图，点D、E分别在△ABC的边AB，AC上．DE∥BC，点G在边BC上，AG交DE于点H，点O是线段AG的中点，若HG2=HO•HA，且DE=7.2，则BC长为9.6．
11．将边长为2的正三角形沿着三条中位线翻折，使得三个顶点重合于同一点，则形成的立体图形的体积为（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{\sqrt{2}}{12}$ | C． | $\frac{\sqrt{3}}{12}$ | D． | $\frac{\sqrt{6}}{24}$ |