Question

15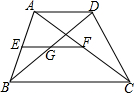．如图，在梯形ABCD中，AD∥BC，E、F分别为AB、AC的中点，BD与EF相交于点G，求证：GF=$\frac{1}{2}$（BC-AD）．

Answer 1

分析 连接AG交BC于点H，由三角形中位线定理可得到EF和BC以及EG和AD的数量关系，进而可求出GF 和BC，AD之间的数量关系．

解答 证明：连接AG交BC于点H，
∵E、F分别为AB、AC的中点，
∴EF是△ABC的中位线，
∴EF∥BC，EF=$\frac{1}{2}$BC，
∴AD∥BC，E是AB中点，
∴AG=FH，
∴EG=$\frac{1}{2}$AD，
∵FG=EF-EG，
∴GF=$\frac{1}{2}$（BC-AD）．

点评 本题考查了三角形的中位线定理，中位线是三角形中的一条重要线段，由于它的性质与线段的中点及平行线紧密相连，因此，它在几何图形的计算及证明中有着广泛的应用．