题目内容
20.已知(-4xm+2ny3m-n)÷(-2x5my2m+n)的商与-$\frac{1}{2}$x3y2是同类项,求m+n的值.分析 先根据整式的除法法则求出(-4xm+2ny3m-n)÷(-2x5my2m+n)的商,再根据同类项的定义列出关于m、n的方程组,进而得出m+n的值.
解答 解:(-4xm+2ny3m-n)÷(-2x5my2m+n)=2x2n-4mym-2n,
根据题意得$\left\{\begin{array}{l}{2n-4m=3}\\{m-2n=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-\frac{5}{3}}\\{n=-\frac{11}{6}}\end{array}\right.$,
则m+n=-$\frac{5}{3}$-$\frac{11}{6}$=-$\frac{7}{2}$.
点评 此题考查了整式的除法,同类项的定义,二元一次方程组的解法,熟练掌握整式的除法法则是解本题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
4.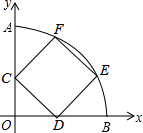 如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在$\widehat{AB}$上),则正方形CDEF的边长为( )
如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在$\widehat{AB}$上),则正方形CDEF的边长为( )
 如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在$\widehat{AB}$上),则正方形CDEF的边长为( )
如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在$\widehat{AB}$上),则正方形CDEF的边长为( )| A. | 3 | B. | $\frac{5(\sqrt{5}-1)}{2}$ | C. | $\sqrt{10}$ | D. | 以上都不正确 |
5.某工厂要建一个面积为130m2的仓库,仓库的一边靠墙(墙长为16m),并在与墙平行的一边开一道1m宽的门,现有能围成32m的木板,求仓库的长与宽?若设垂直于墙的边长为x米,则列出的方程为( )
| A. | x•(32-2x+1)=130 | B. | $\frac{{({32-2x+1})}}{2}•x=130$ | C. | x•(32-2x-1)=130 | D. | $\frac{{({32-2x-1})}}{2}•x=130$ |
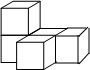 如图所示的几何体是由五个小正方体组合而成的,它的左视图是( )
如图所示的几何体是由五个小正方体组合而成的,它的左视图是( )


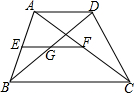 如图,在梯形ABCD中,AD∥BC,E、F分别为AB、AC的中点,BD与EF相交于点G,求证:GF=$\frac{1}{2}$(BC-AD).
如图,在梯形ABCD中,AD∥BC,E、F分别为AB、AC的中点,BD与EF相交于点G,求证:GF=$\frac{1}{2}$(BC-AD).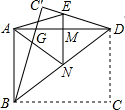 如图,一张宽为3,长为4的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于M,则ME=$\frac{7}{12}$.
如图,一张宽为3,长为4的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于M,则ME=$\frac{7}{12}$.