题目内容
 如图,在平面直角坐标系种,点P在第一象限,⊙P与x轴相切于点Q,与y轴交于N(0,2),M(0,8)两点,反比例函数y=
如图,在平面直角坐标系种,点P在第一象限,⊙P与x轴相切于点Q,与y轴交于N(0,2),M(0,8)两点,反比例函数y=| k |
| x |
考点:反比例函数综合题
专题:
分析:如图,过点P作PE⊥MN于点E,连接PQ.由垂径定理易求EM=NE=3;根据切线的性质可以判定四边形PEOQ为矩形,则PQ=OE=5,PE=OQ.所以在直角△PEM中,根据勾股定理可以求得PE=4,则P(4,5).所以把点P的坐标代入反比例函数解析式来求k的值.
解答: 解:如图,过点P作PE⊥MN于点E,连接PQ.
解:如图,过点P作PE⊥MN于点E,连接PQ.
∵N(0,2),M(0,8),
∴MN=6,
∴EM=NE=3,
∴PQ=OE=5,即⊙P的半径为5.
又∵⊙P与x轴相切于点Q,
∴PQ⊥OQ,
∴四边形PEOQ为矩形,
∴PQ=OE=5,PE=OQ.
在直角△PEM中,由勾股定理,得
PE=
=
=4,
∴P(4,5).
又∵反比例函数y=
经过点P,
∴k=xy=4×5=20.
故答案是:20.
 解:如图,过点P作PE⊥MN于点E,连接PQ.
解:如图,过点P作PE⊥MN于点E,连接PQ.∵N(0,2),M(0,8),
∴MN=6,
∴EM=NE=3,
∴PQ=OE=5,即⊙P的半径为5.
又∵⊙P与x轴相切于点Q,
∴PQ⊥OQ,
∴四边形PEOQ为矩形,
∴PQ=OE=5,PE=OQ.
在直角△PEM中,由勾股定理,得
PE=
| PM2-EM2 |
| 52-32 |
∴P(4,5).
又∵反比例函数y=
| k |
| x |
∴k=xy=4×5=20.
故答案是:20.
点评:此题综合考查了切线的性质、垂径定理,勾股定理以及反比例函数综合题.此题难度适中,注意掌握辅助线的作法,数形结合思想的应用.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C(
已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C(| 2 |
| 3 |
| A、当x<-1时,M=Y1 |
| B、当-1<x<0时,Y2<Y3<Y1 |
| C、当0≤x≤2时,M的最大值是1,无最小值 |
| D、当x≥2时,M最大值是1,无最小值 |

 如图所示,在矩形ABCD中,AB=6,BC=8,将矩形折叠,使点C与点A重合,折痕为EF,再展平,EF与AC相交于点O,连接AF,CE,求折痕EF的长.
如图所示,在矩形ABCD中,AB=6,BC=8,将矩形折叠,使点C与点A重合,折痕为EF,再展平,EF与AC相交于点O,连接AF,CE,求折痕EF的长. 如图,直线AB与CD相交于点O,OE⊥AB,∠COE=30°,求∠DOA的度数.
如图,直线AB与CD相交于点O,OE⊥AB,∠COE=30°,求∠DOA的度数.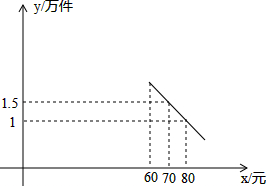 某企业在自主研制新产品的同时考虑招聘员工的计划,已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其他费用15万元,设产品月销售量为y(万件),销售单价为x(元),试销阶段40≤x≤60,企业把试销情况列成表格(见下表),正式销售阶段60<x<100,企业把销售情况绘制成函数关系(见下图).
某企业在自主研制新产品的同时考虑招聘员工的计划,已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其他费用15万元,设产品月销售量为y(万件),销售单价为x(元),试销阶段40≤x≤60,企业把试销情况列成表格(见下表),正式销售阶段60<x<100,企业把销售情况绘制成函数关系(见下图).
 如图,已知AB∥CD,请探索图形中∠P与∠A,∠C的关系,并说明理由.
如图,已知AB∥CD,请探索图形中∠P与∠A,∠C的关系,并说明理由.