题目内容
 如图,在锐角△ABC中,CD,BE分别是AB,AC上的高,且CD,BE交于点P,若∠A=80°,∠BPC的度数是
如图,在锐角△ABC中,CD,BE分别是AB,AC上的高,且CD,BE交于点P,若∠A=80°,∠BPC的度数是考点:多边形内角与外角
专题:
分析:根据垂直的定义可得∠ADP=∠AEP=90°,然后在四边形ADPE中,根据四边形的内角和公式列式计算求出∠DPE的度数,再根据对顶角相等解答.
解答:解:∵CD,BE分别是AB,AC上的高,
∴∠ADP=∠AEP=90°,
又∠A=80°,
∴在四边形ADPE中,∠DPE=(4-2)•180°-80°-90°-90°=100°,
∴∠BPC=∠DPE=100°.
故答案为:100°.
∴∠ADP=∠AEP=90°,
又∠A=80°,
∴在四边形ADPE中,∠DPE=(4-2)•180°-80°-90°-90°=100°,
∴∠BPC=∠DPE=100°.
故答案为:100°.
点评:本题考查了多边形的内角与外角,多边形的内角和公式,对顶角相等的性质,是基础题,求出∠BPC的对顶角的度数是解题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
对于素数p,q,方程x4-px3+q=0有整数解,则p=( )
| A、1 | B、2 | C、3 | D、4 |
一个圆作滚动运动(如图),它从位置A开始,在与它相同的其它六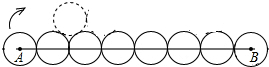 个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.
个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.
 个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.
个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.| A、3 | ||
B、
| ||
C、
| ||
D、
|
有一个六边形的半径为4cm,则这个六边形的面积为( )
A、6
| ||
B、12
| ||
C、24
| ||
D、48
|
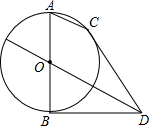 已知:如图,AB为⊙O的直径,弦AC∥OD,BD切⊙O于B,连接CD,
已知:如图,AB为⊙O的直径,弦AC∥OD,BD切⊙O于B,连接CD, 如图,边长为5的菱形ABCD中,AE⊥BC于点E,AE=4.以AE为边向右作正方形AEFG.边GF与CD交于点H,求FH的长.
如图,边长为5的菱形ABCD中,AE⊥BC于点E,AE=4.以AE为边向右作正方形AEFG.边GF与CD交于点H,求FH的长.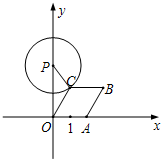 如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,当点A在运动过程中,⊙P与菱形OABC的边所在直线相切时,t=
如图,已知点A从(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O,A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,当点A在运动过程中,⊙P与菱形OABC的边所在直线相切时,t=