��Ŀ����
15��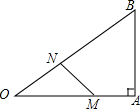 ��ͼ����Rt��OAB�У���A=90�㣬OA=4��AB=3������M�ӵ�A����������M�ӵ�A��������ÿ��1����λ���ȵ��ٶȣ���AO���յ�O�ƶ���ͬʱ��N�ӵ�O��������ÿ��$\frac{5}{4}$����λ���ȵ��ٶȣ���OB���յ�B�ƶ������˶�ʱ��Ϊt�룮
��ͼ����Rt��OAB�У���A=90�㣬OA=4��AB=3������M�ӵ�A����������M�ӵ�A��������ÿ��1����λ���ȵ��ٶȣ���AO���յ�O�ƶ���ͬʱ��N�ӵ�O��������ÿ��$\frac{5}{4}$����λ���ȵ��ٶȣ���OB���յ�B�ƶ������˶�ʱ��Ϊt�룮��1���ú�t�Ĵ���ʽ��ʾ��N��OA�ľ��룻
��2�����OMN�������S����S��t֮��ĺ�������ʽ����xΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
��3�������������˶������У��Ƿ����ijһʱ�̣�ʹ��OMN��ֱ�������Σ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���� ��1���ɹ��ɶ��������OB���������Ǻ������ɣ�
��2���õ�S��t�ĺ�����ϵ���Ӷ�ȷ����������ֵ��
��3��Ҫʹ��OMN��ֱ�������Σ�һ��ֱ�������κ������ƣ����ɣ�
��� �⣺��1����ͼ1��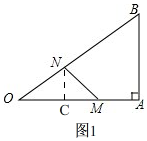 ��Rt��OAB�У�OB=$\sqrt{{OA}^{2}{+AB}^{2}}$=5��
��Rt��OAB��OB=$\sqrt{{OA}^{2}{+AB}^{2}}$=5��
��sin��O=$\frac{AB}{OB}$=$\frac{3}{5}$
���N��OA�ľ���ΪON��sin��O=$\frac{5}{4}$t��$\frac{3}{5}$=$\frac{3}{4}$t��
��2��S=$\frac{1}{2}$��4-t����$\frac{3}{4}$t=-$\frac{3}{8}$t2+$\frac{3}{2}$t=-$\frac{3}{8}$��t-2��2+$\frac{3}{2}$��
��t=2ʱ��S�����ֵ��
���ֵΪS=$\frac{3}{2}$��
��3���ߡ�ABOΪֱ�������Σ�
����M��N��OΪ����������κ͡�ABO����ʱ����OMN��ֱ�������Σ�
����OMN�ס�OABʱ��
��$\frac{OM}{OA}=\frac{ON}{OB}$��
��$\frac{4-t}{4}=\frac{\frac{5}{4}t}{5}$��
��t=2��
����OMN�ס�OBAʱ��
��$\frac{OM}{OB}=\frac{ON}{OA}$��
��$\frac{4-t}{5}=\frac{\frac{5}{4}t}{4}$��
��t=$\frac{64}{41}$��
��t=2��t=$\frac{64}{41}$ʱ����OMN��ֱ��������
���� �����������ε��ۺ��⣬��Ҫ������㵽ֱ�ߵľ��룬���������ε����ʣ��Ȿ��Ĺؼ�����M��N��OΪ����������κ͡�ABO���Ƶ��жϣ�

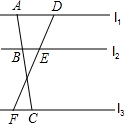 ��ͼ��ֱ��l1��l2��l3��ֱ��AC�ֱ�l1��l2��l3�ڵ�A��B��C��ֱ��DF�ֱ�l1��l2��l3�ڵ�D��E��F����֪AB=2��AC=5��DF=6����DE�ij��ǣ�������
��ͼ��ֱ��l1��l2��l3��ֱ��AC�ֱ�l1��l2��l3�ڵ�A��B��C��ֱ��DF�ֱ�l1��l2��l3�ڵ�D��E��F����֪AB=2��AC=5��DF=6����DE�ij��ǣ�������| A�� | 3 | B�� | $\frac{12}{5}$ | C�� | $\frac{18}{5}$ | D�� | $\frac{5}{2}$ |
| A�� | ����ȷ��һ��ֱ�� | |
| B�� | �Ƚǵ������� | |
| C�� | ��һ������ֻ��һ��ֱ������ֱ֪��ƽ�� | |
| D�� | ����֮�䣬�߶���� |
 ��ͼ��Ϊ�˼���ӵĿ��ȣ�ijѧϰС���ںӶ�ѡ��һ��Ŀ���A�����ںӰ�����һ��ѡȡ��B�͵�C��ʹAB��BC��Ȼ����ѡȡ��E��ʹE C��BC��������ȷ��BC��AE�Ľ���D����ʱ������BD=160 �ף�DC=80�ף�E C=49�ף���A��B��ľ��룮
��ͼ��Ϊ�˼���ӵĿ��ȣ�ijѧϰС���ںӶ�ѡ��һ��Ŀ���A�����ںӰ�����һ��ѡȡ��B�͵�C��ʹAB��BC��Ȼ����ѡȡ��E��ʹE C��BC��������ȷ��BC��AE�Ľ���D����ʱ������BD=160 �ף�DC=80�ף�E C=49�ף���A��B��ľ��룮 С�����������γ�̲Ϳ�μ����ʵ������ھ���P����þ���Bλ����ƫ��45�㷽��Ȼ���ر�ƫ��60�㷽����100���ᄚ��A����ʱ��þ���B����λ�ھ���A�����Ϸ�����A�뾰��B֮��ľ��룮��$\sqrt{3}$ȡ1.73��
С�����������γ�̲Ϳ�μ����ʵ������ھ���P����þ���Bλ����ƫ��45�㷽��Ȼ���ر�ƫ��60�㷽����100���ᄚ��A����ʱ��þ���B����λ�ھ���A�����Ϸ�����A�뾰��B֮��ľ��룮��$\sqrt{3}$ȡ1.73�� ����ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊ1����������Σ������������ߵĽ���������Σ�ABC�Ķ���A��C������ֱ�Ϊ��-4��5������-1��3����
����ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊ1����������Σ������������ߵĽ���������Σ�ABC�Ķ���A��C������ֱ�Ϊ��-4��5������-1��3����