题目内容
14.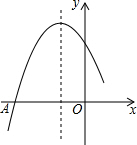 如图是二次函数y=ax2+bx+c的图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①c>0;②b2>4ac;③b=-2a;④a+b+c=0,其中正确结论的番号是①②④.
如图是二次函数y=ax2+bx+c的图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①c>0;②b2>4ac;③b=-2a;④a+b+c=0,其中正确结论的番号是①②④.
分析 ①由抛物线与x轴的交点在y轴正半轴可得出c>0,①正确;②由抛物线与x轴有两个不相同的交点可得出b2-4ac>0,②正确;③由抛物线的对称轴为x=-1可得出b=2a,③错误;④由抛物线的对称轴结合点A的坐标即可得出抛物线与x轴的另一交点坐标为(1,0),进而可得出a+b+c=0,④正确.综上即可得出结论.
解答 解:①∵抛物线与y轴交点在y轴正半轴,
∴c>0,①正确;
②∵抛物线与x轴有两个不同的交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴△=b2-4ac>0,
∴b2>4ac,②正确;
③∵抛物线对称轴为直线x=-1,
∴-$\frac{b}{2a}$=-1,
∴b=2a,③错误;
④∵抛物线对称轴为直线x=-1,且点A的坐标为(-3,0),
∴抛物线与x轴另一交点的坐标为(1,0),
∴当x=1时,y=a+b+c=0,④正确.
综上所述:正确结论的番号是①②④.
故答案为:①②④.
点评 本题考查了二次函数图象与系数的关系,观察二次函数图象找出a、b、c之间的各种关系是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
4.在解方程$\frac{x-1}{2}$=1-$\frac{2x+3}{3}$时,去分母正确的是( )
| A. | 3(x-1)=1-2(2+3x) | B. | 3(x-1)=1+2(2x+3) | C. | 3(x-1)=6-2(2x+3) | D. | 3(x-1)=6+2(2x+3) |
6. 如图,是一个表面标有数字的正方体的展开图,请你指出数字2所在的面所对的面的数字为( )
如图,是一个表面标有数字的正方体的展开图,请你指出数字2所在的面所对的面的数字为( )
 如图,是一个表面标有数字的正方体的展开图,请你指出数字2所在的面所对的面的数字为( )
如图,是一个表面标有数字的正方体的展开图,请你指出数字2所在的面所对的面的数字为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.