题目内容
 一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线成45°角,水流最高点B比喷头A高2米.
一自动喷灌设备的喷流情况如图所示,设水管OA在高出地面1.5米的A处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头A与水流最高点B连线成45°角,水流最高点B比喷头A高2米.(1)求抛物线解析式;
(2)求水流落地点C到O点的距离;
(3)若水流的水平位移(x米)与水流的运动时间(t秒)之间的函数关系为:t=0.8x,求共有几秒钟,水流高度不低于2米.
考点:二次函数的应用
专题:
分析:(1)作BD⊥y轴于点D,由∠DAB=45°,就可以求出AD=BD=2,就可以求出B的坐标,设抛物线的解析式为y=a(x-2)2+3.5,由待定系数法求出其解即可;
(2)当y=0时代入(1)的解析式求出其解即可;
(3)当y=2时代入(1)的解析式求出x的值,再将x的值代入t=0.8x求出t的值即可.
(2)当y=0时代入(1)的解析式求出其解即可;
(3)当y=2时代入(1)的解析式求出x的值,再将x的值代入t=0.8x求出t的值即可.
解答:解:(1)作BD⊥y轴于点D,
∴∠ADB=90°.
∵∠DAB=45°,
∴∠ABD=∠DBA=45°,
∴AD=BD=2,
∴B(2,3.5).
∵OA=1.5,
∴A(0,1.5).
设抛物线的解析式为y=a(x-2)2+3.5,由题意,得
1.5=4a+3.5,
解得:a=-0.5.
∴y=-0.5(x-2)2+3.5.
答:抛物线解析式为y=-0.5(x-2)2+3.5;
(2)当y=0时,
0=-0.5(x-2)2+3.5.
解得:x1=2+
,x2=2-
(舍去),
∴水流落地点C到O点的距离为2+
;
(3)当y=2时,
2=-0.5(x-2)2+3.5.
解得:x3=2+
,x4=2-
,
∴水流位移的距离为:2+
-(2-
)=2
,
∴t=0.8×2
=
,
∴共有
秒钟,水流高度不低于2米.
∴∠ADB=90°.
∵∠DAB=45°,
∴∠ABD=∠DBA=45°,
∴AD=BD=2,
∴B(2,3.5).
∵OA=1.5,
∴A(0,1.5).
设抛物线的解析式为y=a(x-2)2+3.5,由题意,得
1.5=4a+3.5,
解得:a=-0.5.
∴y=-0.5(x-2)2+3.5.
答:抛物线解析式为y=-0.5(x-2)2+3.5;

(2)当y=0时,
0=-0.5(x-2)2+3.5.
解得:x1=2+
| 7 |
| 7 |
∴水流落地点C到O点的距离为2+
| 7 |
(3)当y=2时,
2=-0.5(x-2)2+3.5.
解得:x3=2+
| 3 |
| 3 |
∴水流位移的距离为:2+
| 3 |
| 3 |
| 3 |
∴t=0.8×2
| 3 |
| 8 |
| 5 |
| 3 |
∴共有
| 8 |
| 5 |
| 3 |
点评:本题考查了待定系数法求二次函数的解析式的运用,顶点式的运用,由函数值求自变量的值的运用,一次函数的运用,解答时求出二次函数的解析式是关键.

练习册系列答案
相关题目
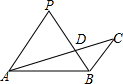 如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )
如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )| A、16 | B、15 | C、7 | D、6 |
一物体及其主视图如图所示,则它的左视图与俯视图分别是图形中的( )


| A、①② | B、③② | C、①④ | D、③④ |
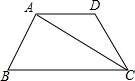 在梯形ABCD中,AD∥BC,AB=AD=DC,∠B=∠BCD=60°,连接AC.求cos∠ACB的值.
在梯形ABCD中,AD∥BC,AB=AD=DC,∠B=∠BCD=60°,连接AC.求cos∠ACB的值.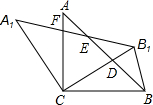 如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F
如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F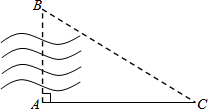 如图,A、B两点在河两岸,为了测算这两点之间的距离,小华在河岸边选定一点C,测得AC=100米,∠A=90°,∠C=30°,则AB≈
如图,A、B两点在河两岸,为了测算这两点之间的距离,小华在河岸边选定一点C,测得AC=100米,∠A=90°,∠C=30°,则AB≈ 已知:△ABC是等腰直角三角形,∠A=90°,BD平分∠ABC交AC于点D,CE⊥BD.
已知:△ABC是等腰直角三角形,∠A=90°,BD平分∠ABC交AC于点D,CE⊥BD. 如图,⊙O为△ABC的外接圆,
如图,⊙O为△ABC的外接圆,