题目内容
19.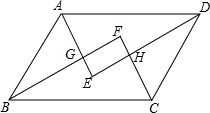 ?ABCD中,AE、CF、BF、DE分别为四个内角平分线,求证:EGFH是矩形.
?ABCD中,AE、CF、BF、DE分别为四个内角平分线,求证:EGFH是矩形.
分析 由平行四边形的性质得出邻角互补,由角平分线的定义得出∠AGB=90°,同理:∠E=∠F=90°,得出∠EGF=90°,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴∠BAD+∠ABC=180°,
∵AE、BF分别是内角的平分线,
∴∠BAG=∠DAG=$\frac{1}{2}$∠BAD,∠ABG=∠CBE=$\frac{1}{2}$∠ABC,
∴∠BAG+∠ABG=$\frac{1}{2}$(∠BAD+∠ABC)=90°,
同理:∠E=∠F=90°,
∴∠EGF=90°,
∴四边形EGFH是矩形.
点评 本题考查了平行四边形的性质、角平分线的定义、矩形的判定;熟练掌握平行四边形的性质,由角平分线的定义求出∠E=∠F=90°是解决问题的突破口.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.一个正数的平方根是x-5和x+1,则x的值为( )
| A. | 2 | B. | -2 | C. | 0 | D. | 无法确定 |
14.抛物线C1:y=x2-4x+8和抛物线C2:y=-x2-8x-18关于点P成中心对称,则点P坐标是( )
| A. | (1,1) | B. | (-1,1) | C. | (-1,-1) | D. | (-3,2) |
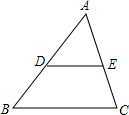 如图,在△ABC中,D、E分别为AB、AC的中点,连接DE,若S△ADE=2,则四边形BDEC的面积为6.
如图,在△ABC中,D、E分别为AB、AC的中点,连接DE,若S△ADE=2,则四边形BDEC的面积为6.