题目内容
6.化简:$\frac{{(y-z)}^{2}}{(x-y)(x-z)}$+$\frac{{(z-x)}^{2}}{(y-x)(y-z)}$+$\frac{{(x-y)}^{2}}{(z-x)(z-y)}$.分析 设x-y=a,y-z=b,x-z=c,得出a+b=x-z=-c,代入后通分,再变形,即可得出答案.
解答 解:设x-y=a,y-z=b,x-z=c,
则a+b=x-z=-c,
$\frac{(y-z)^{2}}{(x-y)(x-z)}$+$\frac{(z-x)^{2}}{(y-x)(y-z)}$+$\frac{(x-y)^{2}}{(z-x)(z-y)}$
=$\frac{{b}^{2}}{ac}$+$\frac{(-c)^{2}}{-ab}$+$\frac{{a}^{2}}{(-c)•(-b)}$
=$\frac{{b}^{2}}{ac}$-$\frac{{c}^{2}}{ab}$+$\frac{{a}^{2}}{bc}$
=$\frac{{b}^{3}-{c}^{3}+{a}^{3}}{abc}$
=$\frac{(a+b)({a}^{2}-ab+{b}^{2})-{c}^{3}}{abc}$
=$\frac{-c({a}^{2}-ab+{b}^{2})-{c}^{3}}{abc}$
=-$\frac{{a}^{2}-ab+{b}^{2}+{c}^{2}}{ab}$
=-$\frac{{a}^{2}-ab+{b}^{2}+[-(a+b)^{2}]}{ab}$
=-$\frac{2{a}^{2}+ab+2{b}^{2}}{ab}$
=-$\frac{2(x-y)^{2}+(x-y)(y-z)+2(y-z)^{2}}{(x-y)(y-z)}$
=$\frac{2{x}^{2}-3xy+3{y}^{2}-xz-3yz+2{z}^{2}}{xy-xz-{y}^{2}+yz}$.
点评 本题考查了分式的加减的应用,能选择适当的方法进行计算是解此题的关键.

练习册系列答案
相关题目
14.抛物线C1:y=x2-4x+8和抛物线C2:y=-x2-8x-18关于点P成中心对称,则点P坐标是( )
| A. | (1,1) | B. | (-1,1) | C. | (-1,-1) | D. | (-3,2) |
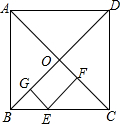 如图,在正方形ABCD中,对角线AC、BD交于O,E点在BC上,EG⊥OB,EF⊥OC,垂足分别为点G、F,AC=10,则EG+EF=5.
如图,在正方形ABCD中,对角线AC、BD交于O,E点在BC上,EG⊥OB,EF⊥OC,垂足分别为点G、F,AC=10,则EG+EF=5.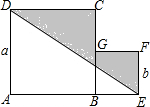 两个边长为a、b的正方形拼成如图所示的形状,连结D、E,求阴影部分的面积.
两个边长为a、b的正方形拼成如图所示的形状,连结D、E,求阴影部分的面积.