题目内容
4.已知$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$-A=$\frac{x}{x+1}$,其中A是一个含x的代数式.(1)求A化简后的结果;
(2)当x满足不等式组$\left\{\begin{array}{l}{x+3>0}\\{x+1≤0}\end{array}\right.$,且x为整数时,求A的值.
分析 (1)原式变形后,通分并利用同分母分式的减法法则计算即可得到结果;
(2)求出不等式组的解集,确定出整数x的值,代入计算即可求出A的值.
解答 解:(1)根据题意得:A=$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$-$\frac{x}{x+1}$=$\frac{(x-1)^{2}}{(x+1)(x-1)}$-$\frac{x}{x+1}$=$\frac{x-1}{x+1}$-$\frac{x}{x+1}$=$\frac{x-1-x}{x+1}$=-$\frac{1}{x+1}$;
(2)不等式组$\left\{\begin{array}{l}{x+3>0}\\{x+1≤0}\end{array}\right.$,得:-3<x≤-1,
∵x为整数,∴x=-2或x=-1,
由A=-$\frac{1}{x+1}$,得到x≠-1,
则当x=-2时,A=-$\frac{1}{x+1}$=1.
点评 此题考查了分式的加减法,以及一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.如果$\sqrt{\frac{x}{x-3}}=\frac{\sqrt{x}}{\sqrt{x-3}}$成立,那么( )
| A. | x≥3 | B. | 0≤x≤3 | C. | x≥0 | D. | x>3 |
13.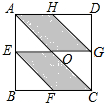 如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )
 如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
14. 如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )
如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )
 如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )
如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )| A. | ∠ABC=∠DCB | B. | AC=DB | C. | ∠A=∠D | D. | OC=OB |
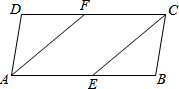 如图,在平行四边形ABCD中,已知AF平分∠DAB,CE平分∠BCD,
如图,在平行四边形ABCD中,已知AF平分∠DAB,CE平分∠BCD,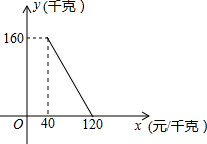 某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售x(元/千克)之间函数关系如图所示.
某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售x(元/千克)之间函数关系如图所示. 如图,在⊙O中,∠C=30°,AB=2cm,则弧AB的长等于$\frac{2π}{3}$.(结果保留π)
如图,在⊙O中,∠C=30°,AB=2cm,则弧AB的长等于$\frac{2π}{3}$.(结果保留π)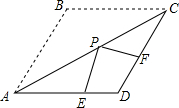 如图,在等腰△ABC中,AB=BC=4,把△ABC沿AC翻折得到△ADC.则
如图,在等腰△ABC中,AB=BC=4,把△ABC沿AC翻折得到△ADC.则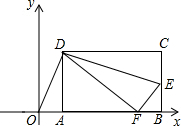 如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(3,4),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点C的坐标为(8,4)或(3$+2\sqrt{5}$,4)或($\frac{43}{6}$,4).
如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(3,4),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点C的坐标为(8,4)或(3$+2\sqrt{5}$,4)或($\frac{43}{6}$,4).