题目内容
14.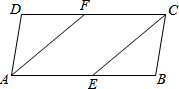 如图,在平行四边形ABCD中,已知AF平分∠DAB,CE平分∠BCD,
如图,在平行四边形ABCD中,已知AF平分∠DAB,CE平分∠BCD,(1)求证:四边形AECF是平行四边形;
(2)请写出与线段AD相等的线段.
分析 (1)直接利用平行四边形的性质得出∠DAB=∠BCD,AB∥DC,AD=BC,DC=AB,进而利用角平分线的性质得出∠DAF=∠DFA,∠BCE=∠BEC,进而得出FC$\stackrel{∥}{=}$AE,即可得出答案;
(2)直接利用等腰三角形的性质进而得出答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,AB∥DC,AD=BC,DC=AB,
∴∠DFA=∠FAB,∠DCE=∠BEC,
∵AF平分∠DAB,CE平分∠BCD,
∴∠DAF=∠FAB,∠DCE=∠BCE,
∴∠DAF=∠DFA,∠BCE=∠BEC,
∴AD=DF,BE=BC,
∴DC-DF=AB-BE,
∴FC=AE,
即FC$\stackrel{∥}{=}$AE,
∴四边形AECF是平行四边形;
(2)解:由(1)得:AD=DF,BC=BE,AD=BC,
故AD=DF=BC=BE,
即与线段AD相等的线段有:DF,BC,BE.
点评 此题主要考查了平行四边形的判定与性质以及等腰三角形的性质,正确掌握平行四边形的性质是解题关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
19.若${({2+y})^2}+\sqrt{x+y-1}=0$,则xy的值等于( )
| A. | -6 | B. | -2 | C. | 2 | D. | 6 |
 如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°.
如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°.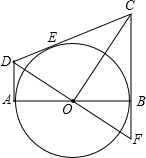 如图,从圆O外的两点C和D分别引圆的两条切线DA,DC,CB,切点分别是A、E和B,AB是圆O的直径,连接OC、OD,延长DO交CB的延长线于点F,给出如下结论:①AD+BC=CD;②OD2=DE•CD;③CO=DF;④△AOD∽△BCO,其中正确的是①②④.(把所有正确的序号都填在横线上).
如图,从圆O外的两点C和D分别引圆的两条切线DA,DC,CB,切点分别是A、E和B,AB是圆O的直径,连接OC、OD,延长DO交CB的延长线于点F,给出如下结论:①AD+BC=CD;②OD2=DE•CD;③CO=DF;④△AOD∽△BCO,其中正确的是①②④.(把所有正确的序号都填在横线上).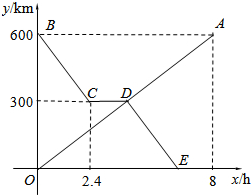 货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.
货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.