题目内容
12.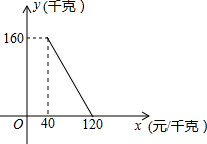 某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售x(元/千克)之间函数关系如图所示.
某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售x(元/千克)之间函数关系如图所示.(1)求y与x函数关系式;
(2)商店想在销售成本不超过3800元的情况下,使销售利润达到3000元,销售单价应定为多少?
分析 (1)根据函数图象可以设出函数解析式,函数图象过点(40,160),(120,0),从而可以求出函数的解析式;
(2)根据题意可以列出相应的方程和不等式,从而可以解答本题.
解答 解:(1)设y与x之间的函数关系式为y=kx+b,
则$\left\{\begin{array}{l}{40k+b=160}\\{120k+b=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-2}\\{b=240}\end{array}\right.$,
即y与x函数关系式是y=-2x+240;
(2)商店想在销售成本不超过3800元的情况下,使销售利润达到3000元,设销售单价应定为x元/千克,
(x-40)×(-2x+240)=3000,
解得,x=70或x=90,
又∵40(-2x+240)≤3800,
解得,x≥72.5,
故x=90,
即商店想在销售成本不超过3800元的情况下,使销售利润达到3000元,销售单价应定为90元.
点评 本题考查一次函数的应用,解题的关键是明确题意,列出相应的方程和不等式,利用数形结合的思想解答问题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
2.当a=-1时,分式$\frac{{{a^2}+a}}{{{a^2}-a}}$( )
| A. | 等于零 | B. | 等于1 | C. | 等于-1 | D. | 没有意义 |
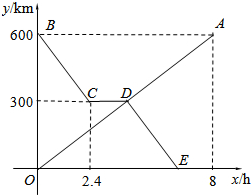 货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.
货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系. 如图1所示的是一个长方形纸带,∠DEF=25°,将纸带沿EF折叠成图2,则图2中的∠BGE的度数是50°.
如图1所示的是一个长方形纸带,∠DEF=25°,将纸带沿EF折叠成图2,则图2中的∠BGE的度数是50°.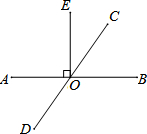 如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.
如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.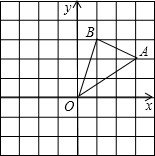 如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A,B的坐标分别是(3,2)、B(1,3).
如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A,B的坐标分别是(3,2)、B(1,3).