题目内容
5.观察下面一组式子:(1)1×$\frac{1}{2}=1-\frac{1}{2}$;(2)$\frac{1}{2}×\frac{1}{3}=\frac{1}{2}-\frac{1}{3}$;
(3)$\frac{1}{3}×\frac{1}{4}=\frac{1}{3}-\frac{1}{4}$;(4)$\frac{1}{4}×\frac{1}{5}=\frac{1}{4}-\frac{1}{5}$…
写出这组式子中的第(n)组式子是$\frac{1}{n}×\frac{1}{n+1}=\frac{1}{n}-\frac{1}{n+1}$.
分析 观察题中算式与结果,若把1看作$\frac{1}{1}$,则算式中的两个因数的分子都是1,分母为连续自然数,结果恰是算式中的第一个因数减去第二个因数,结合此规律即可求解.
解答 解:若把1看作$\frac{1}{1}$,则算式中的两个因数的分子都是1,分母为连续自然数,结果恰是算式中的第一个因数减去第二个因数,
所以第(n)组式子是$\frac{1}{n}×\frac{1}{n+1}=\frac{1}{n}-\frac{1}{n+1}$.
故答案为:$\frac{1}{n}×\frac{1}{n+1}=\frac{1}{n}-\frac{1}{n+1}$.
点评 此题主要考察数的规律探索,结合已知发现总结算式中数的规律,并合理应用是解题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
16.下列关系式中:①y=2x;$②\frac{y}{x}=5$;③y=-$\frac{7}{x}$;④y=5x+1;⑤y=x2-1;⑥y=$\frac{1}{{x}^{2}}$;⑦xy=11,y是x的反比例函数的共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
20.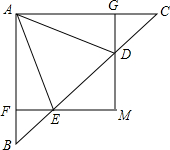 如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
 如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )| A. | △CAE∽△BDA | B. | $\frac{AD}{AE}=\frac{AC}{BD}$ | C. | BD•CE=4 | D. | BE=$\sqrt{2}$BF |
10.(-1)2015的值是( )
| A. | -1 | B. | 1 | C. | -2015 | D. | 2015 |
14.三角形中,三个内角的比为1:3:6,它的三个外角的比为( )
| A. | 1:3:6 | B. | 6:3:1 | C. | 9:7:4 | D. | 4:7:9 |
15. 如图所示的几何体,它的主视图是( )
如图所示的几何体,它的主视图是( )
 如图所示的几何体,它的主视图是( )
如图所示的几何体,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
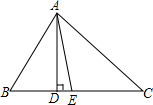 如图,在△ABC中,∠B=63°,∠C=47°,AD和AE分别是它的高和角平分线,则
如图,在△ABC中,∠B=63°,∠C=47°,AD和AE分别是它的高和角平分线,则