题目内容
15.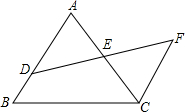 如图,AB∥CF,E为DF中点,AB=20,CF=15,则BD=5.
如图,AB∥CF,E为DF中点,AB=20,CF=15,则BD=5.
分析 根据平行的性质求得内错角相等,已知对顶角相等,又知E是DF的中点,所以根据ASA得出△ADE≌△CFE,从而得出AD=CF,已知AB,CF的长,那么BD的长就不难求出.
解答 解:∵AB∥FC,
∴∠ADE=∠EFC,
∵E是DF的中点,
∴DE=EF,
在△ADE与△CFE中,
$\left\{\begin{array}{l}{∠ADE=∠EFC}\\{DE=EF}\\{∠AED=∠CEF}\end{array}\right.$,
∴△ADE≌△CFE,
∴AD=CF,
∵AB=20,CF=15,
∴BD=AB-AD=20-15=5.
故答案为:5.
点评 本题主要考查全等三角形的判定和性质,平行线的性质,解题的关键在于求证△ADE≌△CFE.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
20.一元二次方程x2+x+1=0的根的情况为( )
| A. | 有两个相等的实数根 | B. | 没有实根 | ||
| C. | 只有一个实数根 | D. | 有两个不相等的实数根 |
6.点A(-3,5)关于原点的对称点的坐标为( )
| A. | (3,5) | B. | (-3,-5) | C. | (3,-5) | D. | (5,-3) |
3.下列各数中,最大的数是( )
| A. | 0 | B. | -1 | C. | -2 | D. | 1 |
10.在$\frac{1}{x}$,$\frac{1}{2}$,$\frac{x+1}{2}$,$\frac{xy}{π}$,$\frac{3}{x+y}$中,分式的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
20.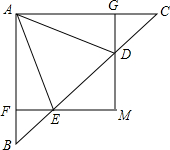 如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
 如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )| A. | △CAE∽△BDA | B. | $\frac{AD}{AE}=\frac{AC}{BD}$ | C. | BD•CE=4 | D. | BE=$\sqrt{2}$BF |
7.下列个数中,负数是( )
| A. | 5 | B. | 0.56 | C. | -3 | D. | +9 |
