双曲线y=(1-m)x${\;}^{{m}^{2}-5}$.当x＞0时.y随x的增大而减小.则m=( )A．2B．-2C．-2或者2D．4 题目和参考答案——青夏教育精英家教网——

题目内容

1．双曲线y=（1-m）x${\;}^{{m}^{2}-5}$，当x＞0时，y随x的增大而减小，则m=（　　）

A．

2

B．

-2

C．

-2或者2

D．

4

分析根据反比例函数的定义列出方程求解，再根据它的性质决定解的取舍．

解答解：根据题意可得：
$\left\{\begin{array}{l}{{m}^{2}-5=-1}\\{1-m＞0}\end{array}\right.$，
解得m=-2，
故选B．

点评本题考查了反比例函数的性质．对于反比例函数y=$\frac{k}{x}$，当k＞0时，在每一个象限内，函数值y随自变量x的增大而减小；当k＜0时，在每一个象限内，函数值y随自变量x增大而增大．

练习册系列答案

蓉城课堂给力A加动力源期末暑假作业四川师范大学电子出版社系列答案

高效A计划期末暑假衔接中南大学出版社系列答案

育文书业期末暑假一本通浙江工商大学出版社系列答案

时刻准备着假期作业暑假原子能出版社系列答案

文诺文化暑假作业快乐假期延边人民出版社系列答案

暑假乐园辽宁师范大学出版社系列答案

伴你成长暑假作业江苏凤凰美术出版社系列答案

赢在暑假抢分计划合肥工业大学出版社系列答案

暑假衔接暑假培优衔接16讲江苏凤凰美术出版社系列答案

浙大优学小学年级衔接捷径浙江大学出版社系列答案

相关题目

11．下列各式：①2x=0②2x-y③$\frac{y-1}{2}$=$\frac{y}{3}$+2④$\frac{5}{x}$+$\frac{2}{x}$=7中，是一元一次方程的是①③（填代号）．

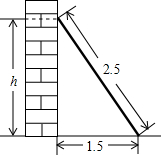如图，长2.5m的梯子靠在墙上，梯子的底部离墙的底端1.5m．
（1）求梯子的顶端与地面的距离h；
（2）由于地面有水，梯子底部向右滑动，梯子顶端随之向下滑动，小明发现梯子底部向右滑动了0.5m，他认为梯子顶端也向下了0.5m．你赞同小明的看法吗？说说你的理由．

如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．△AOB绕点O逆时针旋转90°后得到△A₁OB₁．
（1）画出旋转后的图形；
（2）点A₁的坐标为（-2，3）；
（3）在旋转过程中，点B经过的路径为弧BB₁，求弧BB₁的长为多少．

16．当x为何值时，$\frac{2}{5}$x+$\frac{x-1}{2}$和$\frac{8}{5}$x-$\frac{3（x-1）}{2}$的值互为相反数？

6．已知y是关于x的一次函数，当x=0时，y=-1；当x=-1时，y=-2．y关于x的函数表达式为y=x-1．

13．为了解学生参加体育活动的情况，锦江区某中学德育处对本校部分学生进行了随机问卷调查，其中一个问题是“你平均每天参加体育活动的时间是多少？”共有如下四个选项：
A.0.5小时以下；B.0.5～1小时（不包含1小时）；C.1～1.5小时（包含1小时）；D.1.5小时以上
图①、图②是根据调查结果绘制的两幅不完整的统计图，请你根据统计图提供的信息解答以下问题：
（1）试问本次问卷调查一共调查了多少名学生？
（2）请将图①的条形统计图补充完整；
（3）求在图②的扇形统计图中，C部分所对应的圆心角的度数；
（4）若全校有2000名学生，请你估计全校可能有多少名学生平均每天参加体育活动时间在1小时以上（包含1小时）？

10．若|a-4|+$\sqrt{6+b}$=0，那么a-b的平方根是±$\sqrt{10}$．

11．$\frac{{a}^{2}+a-2}{{a}^{2}+3a+2}$•5（a+1）²等于（　　）