题目内容
10.若|a-4|+$\sqrt{6+b}$=0,那么a-b的平方根是±$\sqrt{10}$.分析 根据非负数的性质求出a、b的值,根据平方根的概念解答即可.
解答 解:由题意得,a-4=0,6+b=0,
解得,a=4,b=-6,
则a-b=10,
故a-b的平方根是±$\sqrt{10}$,
故答案为:±$\sqrt{10}$.
点评 本题考查的是非负数的性质、平方根的概念,掌握非负数之和等于0时,各项都等于0是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.双曲线y=(1-m)x${\;}^{{m}^{2}-5}$,当x>0时,y随x的增大而减小,则m=( )
| A. | 2 | B. | -2 | C. | -2或者2 | D. | 4 |
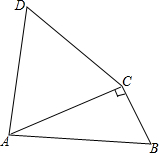 如图,△ABC中,∠ACB=90°,以AC为边作等边△ADC.
如图,△ABC中,∠ACB=90°,以AC为边作等边△ADC.