题目内容
 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,小于
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,小于| 1 |
| 2 |
| 3 |
考点:角平分线的性质,等腰三角形的判定与性质
专题:
分析:由AB∥CD,得出∠MAB=∠CMA,AM是∠CAB的平分线,∠MAB=∠CAM,得出∠CAM=∠CMA,得出△ACM为等腰三角形,再由CN⊥AM三线合一求得AN=AM,故S△ACN=
S△ACM,设点N到AC的距离为h,根据三角形的面积公式求出h的值,进而可得出结论.
| 1 |
| 2 |
解答:解::∵AB∥CD,
∴∠MAB=∠CMA,
∵AM是∠CAB的平分线,
∴∠MAB=∠CAM,
∴∠CAM=∠CMA,
∴CA=CM,
又∵CN⊥AM,
∴AN=MN,
∴S△ACN=
S△ACM=
.
设点N到AC的距离为h,则
AC•h=
,即
×2h=
,解得h=
.
∵角平分线上的点到角两边的距离相等,
∴点N到AB边的距离为
.
故答案为:
.
∴∠MAB=∠CMA,
∵AM是∠CAB的平分线,
∴∠MAB=∠CAM,
∴∠CAM=∠CMA,
∴CA=CM,
又∵CN⊥AM,
∴AN=MN,
∴S△ACN=
| 1 |
| 2 |
| 3 |
设点N到AC的距离为h,则
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
∵角平分线上的点到角两边的距离相等,
∴点N到AB边的距离为
| 3 |
故答案为:
| 3 |
点评:本题考查的是角平分线的性质,熟知角平分线上的点到角两边的距离相等是解答此题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
关于x的不等式ax2-(a2+1)x+a>0(a≠0)的解集为( )
A、x<
| ||
| B、x≠1的实数 | ||
C、
| ||
| D、以上都不对 |
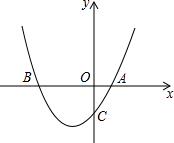 如图,已知二次函数y=ax2+bx+c经过点A(1,0),C(0,3),且对称轴为直线x=-1.
如图,已知二次函数y=ax2+bx+c经过点A(1,0),C(0,3),且对称轴为直线x=-1. 如图,直线AB,CD相交于点O,OE平分∠BOC,FO⊥CD于点O,若∠BOD:∠EOB=2:3,求∠AOF的度数.
如图,直线AB,CD相交于点O,OE平分∠BOC,FO⊥CD于点O,若∠BOD:∠EOB=2:3,求∠AOF的度数. 如图,已知∠AOC=108°,∠BOC=36°,试判断图中哪两个角互为补角,并说明理由.
如图,已知∠AOC=108°,∠BOC=36°,试判断图中哪两个角互为补角,并说明理由.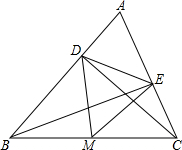 已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M是线段BC的中点,连接DM,EM.
已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M是线段BC的中点,连接DM,EM.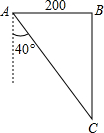 如图,东西两炮台A、B相距2000米,同时发现入侵舰C,炮台A测得敌舰C在它的南偏东40°的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离分别是多少米?(精确到1米)
如图,东西两炮台A、B相距2000米,同时发现入侵舰C,炮台A测得敌舰C在它的南偏东40°的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离分别是多少米?(精确到1米) 如图,P是⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.
如图,P是⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.