题目内容
关于x的不等式ax2-(a2+1)x+a>0(a≠0)的解集为( )
A、x<
| ||
| B、x≠1的实数 | ||
C、
| ||
| D、以上都不对 |
考点:二次函数与不等式(组)
专题:
分析:求出抛物线y=ax2-(a2+1)x+a与x轴的交点,然后根据a的取值范围分情况讨论.
解答:解:令y=0,则ax2-(a2+1)x+a=0,
解得x1=
,x2=a,
所以,抛物线y=ax2-(a2+1)x+a与x轴的交点坐标为(
,0),(a,0),
若a<-1,则不等式的解集是a<x<
,
若a=-1,则不等式无解,
若-1<a<0,则不等式的解集是
<x<a,
若0<a<1,则不等式的解集是x<a或x>
,
若a=1,则不等式的解集是x≠1的实数,
若a>1,则不等式的解集是x<
或x>a,
综上所述,A、B、C选项都不正确.
故选D.
解得x1=
| 1 |
| a |
所以,抛物线y=ax2-(a2+1)x+a与x轴的交点坐标为(
| 1 |
| a |
若a<-1,则不等式的解集是a<x<
| 1 |
| a |
若a=-1,则不等式无解,
若-1<a<0,则不等式的解集是
| 1 |
| a |
若0<a<1,则不等式的解集是x<a或x>
| 1 |
| a |
若a=1,则不等式的解集是x≠1的实数,
若a>1,则不等式的解集是x<
| 1 |
| a |
综上所述,A、B、C选项都不正确.
故选D.
点评:本题考查了二次函数与不等式,难点在于根据a的取值范围分情况讨论.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
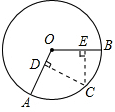 如图,点C是
如图,点C是
 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,小于
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,小于 如图,在六边形ABCDEF中,所有角都相等.
如图,在六边形ABCDEF中,所有角都相等. 如图,已知在?ABCD中,AB=8cm,BC=10cm,∠B=30°,求:
如图,已知在?ABCD中,AB=8cm,BC=10cm,∠B=30°,求: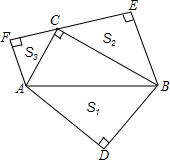 如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC、AC为斜边向外作等腰直角三角形,设所作的△ABD、△BCE、△ACF的面积分别为S1、S2、S3,求证:S1=S2+S3.
如图,在Rt△ABC中,∠ACB=90°,分别以AB、BC、AC为斜边向外作等腰直角三角形,设所作的△ABD、△BCE、△ACF的面积分别为S1、S2、S3,求证:S1=S2+S3. 如图所示,若∠3=∠1+∠2,试猜想AB与CD之间关系?
如图所示,若∠3=∠1+∠2,试猜想AB与CD之间关系? 如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试画出一个三角形使边长为3
如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试画出一个三角形使边长为3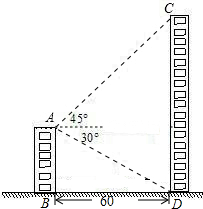 如图,小明在顶楼A处测得对面大楼楼顶点C处的仰角为45°,楼底点D处的俯角为30°,若两座楼AB与CD相距60米,求楼CD的高度约为多少米(结果保留三个有效数字).
如图,小明在顶楼A处测得对面大楼楼顶点C处的仰角为45°,楼底点D处的俯角为30°,若两座楼AB与CD相距60米,求楼CD的高度约为多少米(结果保留三个有效数字).