题目内容
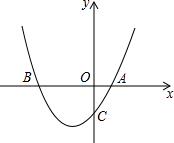 如图,已知二次函数y=ax2+bx+c经过点A(1,0),C(0,3),且对称轴为直线x=-1.
如图,已知二次函数y=ax2+bx+c经过点A(1,0),C(0,3),且对称轴为直线x=-1.(1)求二次函数的表达式;
(2)在抛物线上是否存在点P,使△PAB得面积为10,请写出所有点P的坐标.
考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征
专题:
分析:(1)根据题意列出a,b,c的方程组,求出方程组的解得到a,b,c的值,即可确定出顶点坐标.
(2)由于三角形PAB的面积为10,可得出P点纵坐标的绝对值.可将其代入抛物线的解析式中即可求出P点的坐标.
(2)由于三角形PAB的面积为10,可得出P点纵坐标的绝对值.可将其代入抛物线的解析式中即可求出P点的坐标.
解答:解:(1)根据题意得:
,
解得:a=1,b=2,c=-3,
∴抛物线解析式为y=x2+2x-3.
(2)令y=0,则x2+2x-3=0,
解得x=1或x=-3,
∴AB=4,
∵△PAB得面积为10,设P的纵坐标为h,
∴
AB×|h|=10,
∴|h|=5,
∵y=x2+2x-3=(x+1)2-4,
∴顶点坐标为(-1,-4),
∴P的纵坐标不能为-5,
∴,h=5,
代入得5=x2+2x-3,
解得x=2,x=-4;
∴点P的坐标为(2,5),(-4,5).
|
解得:a=1,b=2,c=-3,
∴抛物线解析式为y=x2+2x-3.
(2)令y=0,则x2+2x-3=0,
解得x=1或x=-3,
∴AB=4,
∵△PAB得面积为10,设P的纵坐标为h,
∴
| 1 |
| 2 |
∴|h|=5,
∵y=x2+2x-3=(x+1)2-4,
∴顶点坐标为(-1,-4),
∴P的纵坐标不能为-5,
∴,h=5,
代入得5=x2+2x-3,
解得x=2,x=-4;
∴点P的坐标为(2,5),(-4,5).
点评:此题考查了待定系数法求二次函数解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
 如图,在数轴上的a,b,c三个实数,且|a|>c>|b|,化简|a-b|-2|a+c|+|c-b|=
如图,在数轴上的a,b,c三个实数,且|a|>c>|b|,化简|a-b|-2|a+c|+|c-b|=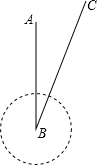 据气象观测,某台风中心正位于城市A正南方向220km的B处,其中心最大风力为12级,每远离台风中心20km,风力就会减弱一级,该台风中心现以15km/h的速度沿北偏东30°的BC方向移动,且台风中心风力不变,若城市所受风力达到或超过4级,则会受台风影响.
据气象观测,某台风中心正位于城市A正南方向220km的B处,其中心最大风力为12级,每远离台风中心20km,风力就会减弱一级,该台风中心现以15km/h的速度沿北偏东30°的BC方向移动,且台风中心风力不变,若城市所受风力达到或超过4级,则会受台风影响.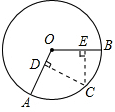 如图,点C是
如图,点C是
 如图,移动平行四边形木架的三条边,使其构成矩形.若矩形面积是原平行四边形面积的2倍,求平行四边形两邻边的夹角α(锐角)的度数.
如图,移动平行四边形木架的三条边,使其构成矩形.若矩形面积是原平行四边形面积的2倍,求平行四边形两邻边的夹角α(锐角)的度数.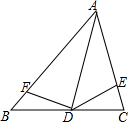 如图,CE=BF,且S△DCE=S△DBF,求证:AD平分∠BAC.
如图,CE=BF,且S△DCE=S△DBF,求证:AD平分∠BAC.
 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,小于
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,小于 如图所示,若∠3=∠1+∠2,试猜想AB与CD之间关系?
如图所示,若∠3=∠1+∠2,试猜想AB与CD之间关系?