Question

4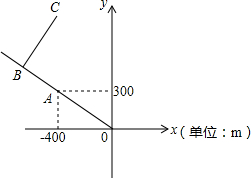．如图是根据宝塔山公园的平面示意图建立的平面直角坐标系，公园的入口位于坐标原点O，古塔位于点A（-400，300），从古塔出发沿射线OA方向前行300m是盆景园B，从盆景园B向右转90°后直行400m到达樱花园C，则点C的坐标是（-400，800）．

Answer 1

分析 根据题意结合全等三角形的判定与性质得出△AOD≌△ACB（SAS），进而得出C，A，D也在一条直线上，求出CD的长即可得出C点坐标．

解答 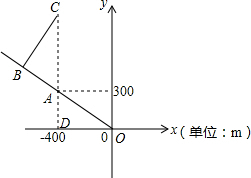解：连接AC，
由题意可得：AB=300m，BC=400m，
在△AOD和△ACB中
∵$\left\{\begin{array}{l}{AD=AB}\\{∠ODA=∠ABC}\\{DO=BC}\end{array}\right.$，
∴△AOD≌△ACB（SAS），
∴∠CAB=∠OAD，
∵B、O在一条直线上，
∴C，A，D也在一条直线上，
∴AC=AO=500m，则CD=AC+AD=800m，
∴C点坐标为：（-400，800）．
故答案为：（-400，800）．

点评 此题主要考查了全等三角形的判定与性质以及勾股定理，得出C，A，D也在一条直线上是解题关键．