题目内容
15．
如图，已知圆心角∠BOC=80°，则圆周角∠BAC的度数是（ ）| A． | 160° | B． | 80° | C． | 40° | D． | 20° |
分析 由圆心角∠BOC=80°，根据圆周角的性质，即可求得圆周角∠BAC的度数．
解答 解：∵圆心角∠BOC=80°，
∴圆周角∠BAC=$\frac{1}{2}$∠BOC=40°．
故选C．
点评 此题考查了圆周角定理．注意在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
金钥匙试卷系列答案
相关题目
19．下列分式中，最简分式是（ ）
| A． | $\frac{6}{15x}$ | B． | $\frac{x-2}{3x-6}$ | C． | $\frac{x+1}{2x+1}$ | D． | $\frac{{a}^{2}-{b}^{2}}{a+b}$ |
如图，沿着方格线，把下列图形分割成四个全等的图形．
3．
如图，AC与BD交于O点，∠1=∠2，下列不能使△ABO≌△DCO的条件是（ ）
如图，AC与BD交于O点，∠1=∠2，下列不能使△ABO≌△DCO的条件是（ ）| A． | ∠A=∠D | B． | AC=BD | C． | AB=DC | D． | ∠ABC=∠DCB |
20．计算15°23′×4的结果是（ ）
| A． | 60°92′ | B． | 60.92° | C． | 60°32′ | D． | 61°32′ |
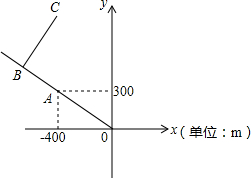如图是根据宝塔山公园的平面示意图建立的平面直角坐标系，公园的入口位于坐标原点O，古塔位于点A（-400，300），从古塔出发沿射线OA方向前行300m是盆景园B，从盆景园B向右转90°后直行400m到达樱花园C，则点C的坐标是（-400，800）．
5．已知两点A（5，6），B（7，2），先将线段AB向左平移一个单位，再以原点O为位似中心，将其缩小为原来的$\frac{1}{2}$得到线段CD，则点A的对应点C的坐标为（ ）
| A． | （2，3） | B． | （-2，-3） | C． | （2，3）或（-2，-3） | D． | （3，3）或（-3，-3） |