题目内容
已知抛物线y=x2+bx+c与直线y=x+3交于点(m,4)、(-2,n),若上下平移后使得抛物线与y=x+3只有一个交点,求平移后的解析式.
考点:二次函数图象与几何变换
专题:几何变换
分析:先利用直线y=x+3确定抛物线y=x2+bx+c与直线y=x+3交点坐标为(1,4),(-2,1),再利用待定系数法求出抛物线解析式为y=x2+2x+1,配成顶点式为y=(x+1)2,根据抛物线上下平移规律,可设抛物线解析式为y=(x+1)2上下平移后的抛物线解析式为y=(x+1)2+m,然后利用根据二次函数与一次函数交点问题得到
只有一组解,再把方程组的解的问题转化为一元二次方程解的问题,最后根据根判别式的意义得到关于m的方程,解方程求出m的值,从而得到平移后的抛物线解析式.
|
解答:解:把点(m,4)、(-2,n)分别代入y=x+3得m+3=4,-2+3=n,
解得m=1,n=1,
则抛物线y=x2+bx+c与直线y=x+3交点坐标为(1,4),(-2,1),
把(1,4),(-2,1)代入y=x2+bx+c得
,
解得
,
所以抛物线解析式为y=x2+2x+1=(x+1)2,
设抛物线解析式为y=(x+1)2上下平移后的抛物线解析式为y=(x+1)2+m,
因为抛物线y=(x+1)2+m与y=x+3只有一个交点,则
只有一组解,
所以关于x的方程x2+x+m-2=0有相等的实数解,则△=1-4(m-2)=0,解得m=
,
所以平移后的抛物线解析式为y=(x+1)2+
.
解得m=1,n=1,
则抛物线y=x2+bx+c与直线y=x+3交点坐标为(1,4),(-2,1),
把(1,4),(-2,1)代入y=x2+bx+c得
|
解得
|
所以抛物线解析式为y=x2+2x+1=(x+1)2,
设抛物线解析式为y=(x+1)2上下平移后的抛物线解析式为y=(x+1)2+m,
因为抛物线y=(x+1)2+m与y=x+3只有一个交点,则
|
所以关于x的方程x2+x+m-2=0有相等的实数解,则△=1-4(m-2)=0,解得m=
| 9 |
| 4 |
所以平移后的抛物线解析式为y=(x+1)2+
| 9 |
| 4 |
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
方程(x-5)(x+1)=x-5的解是( )
| A、x=0 |
| B、x=5 |
| C、x=5或x=--1 |
| D、x=5或x=0 |
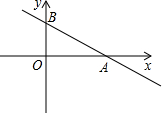 在平面直角坐标系中,点O为坐标原点,直线y=-
在平面直角坐标系中,点O为坐标原点,直线y=-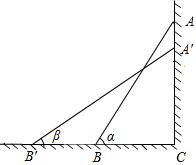 如图,AB是斜靠在墙上的长梯,AB与地面的夹角为α,当梯顶A下滑1m至A′时,梯脚B滑至B′,A′B′与地面的夹角为β,若tanα=
如图,AB是斜靠在墙上的长梯,AB与地面的夹角为α,当梯顶A下滑1m至A′时,梯脚B滑至B′,A′B′与地面的夹角为β,若tanα= 如图,AB是半圆的直径,以半圆的一条弦BC(非直径)为对称轴将BC弧折叠,点D是折叠后的弧BC上一点.若∠ABC=20°,则∠CDB为
如图,AB是半圆的直径,以半圆的一条弦BC(非直径)为对称轴将BC弧折叠,点D是折叠后的弧BC上一点.若∠ABC=20°,则∠CDB为