题目内容
17.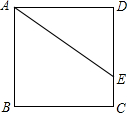 如图,已知正方形ABCD,点E在边DC上,DE=4,EC=2,则AE的长为$\sqrt{52}$.
如图,已知正方形ABCD,点E在边DC上,DE=4,EC=2,则AE的长为$\sqrt{52}$.
分析 在RT△ADE中,利用勾股定理AE=$\sqrt{A{D}^{2}+E{D}^{2}}$即可解决问题.
解答 解:如图,
∵四边形ABCD是正方形,
∴AD=DC,∠D=90°,
∵DE=4,EC=2,
∴AD=CD=6,
在RT△ADE中,∵∠D=90°,AD=6.DE=4,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{{6}^{2}+{4}^{2}}$=$\sqrt{52}$.
故答案为$\sqrt{52}$.
点评 本题考查正方形的性质、勾股定理等知识,解题的关键是利用勾股定理解决问题,属于基础题,中考常考题型.

练习册系列答案
相关题目
9.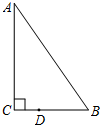 如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
 如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )| A. | 70° | B. | 70°或120° | C. | 120° | D. | 80° |
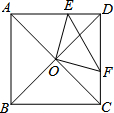 如图,在正方形ABCD中,O是对角线的交点,过点O作OE⊥OF,分别交AD,CD于E,F,若AE=6,CF=4,则EF=2$\sqrt{13}$.
如图,在正方形ABCD中,O是对角线的交点,过点O作OE⊥OF,分别交AD,CD于E,F,若AE=6,CF=4,则EF=2$\sqrt{13}$.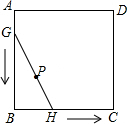 如图,正方形ABCD的边长为4,线段GH=AB,将GH的两端放在正方形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点H从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段GH的中点P所经过的路线围成的图形的面积为16-4π.
如图,正方形ABCD的边长为4,线段GH=AB,将GH的两端放在正方形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点H从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段GH的中点P所经过的路线围成的图形的面积为16-4π.