题目内容
15.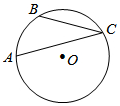 如图,点A、B、C在半径为12的⊙O上,弧AB的弧长为4π,则∠ACB的大小是30°.
如图,点A、B、C在半径为12的⊙O上,弧AB的弧长为4π,则∠ACB的大小是30°.
分析 连结OA、OB.先由弧AB的弧长为4π,利用弧长计算公式求出∠AOB=60°,再根据在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半得到∠ACB=$\frac{1}{2}$∠AOB=30°.
解答 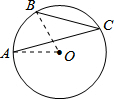 解:连结OA、OB.设∠AOB=n°.
解:连结OA、OB.设∠AOB=n°.
∵弧AB的弧长为4π,
∴$\frac{nπ×12}{180}$=4π,
∴n=60,
∴∠AOB=60°,
∴∠ACB=$\frac{1}{2}$∠AOB=30°.
故答案为30°.
点评 本题考查了弧长公式:l=$\frac{nπr}{180}$(弧长为l,圆心角度数为n,圆的半径为r),同时考查了圆周角定理.

练习册系列答案
相关题目
10.某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表所示,则棉花纤维长度的数据在16≤x<32这个范围的频率为( )
| 棉花纤维长度x | 频数 |
| 0≤x<8 | 1 |
| 8≤x<16 | 2 |
| 16≤x<24 | 8 |
| 24≤x<32 | 6 |
| 32≤x<40 | 3 |
| A. | 0.8 | B. | 0.7 | C. | 0.4 | D. | 0.2 |
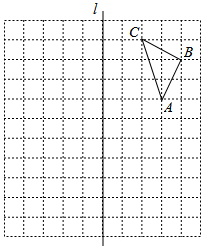 如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点). 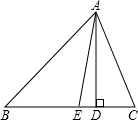 如图,在△ABC中,AD是边BC上的高,AE平分∠BAC,∠B=40°,∠C=68°,求∠AEC和∠DAE的度数.
如图,在△ABC中,AD是边BC上的高,AE平分∠BAC,∠B=40°,∠C=68°,求∠AEC和∠DAE的度数.