题目内容
10．已知二次函数y=（m-2）x2-4mx+2m-6的图象与x轴负半轴至少有一个交点，则m的取值范围为（ ）| A． | 1＜m＜3 | B． | 1≤m＜2或2＜m＜3 | C． | m＜1 | D． | m＞3 |
分析 函数y=（m-2）x2-4mx+2m-6的图象与x轴的负半轴至少有一个交点，分两种情况，一是有两个交点只有一个在负半轴，二是交点都在负半轴，分类解答即可．
解答 解：∵二次函数y=（m-2）x2-4mx+2m-6，
∴m-2≠0，
∴m≠2，
当①图象与x轴的交点有两个，原点的两侧各有一个，
则$\left\{\begin{array}{l}{△＞0}\\{{x}_{1}{x}_{2}＜0}\end{array}\right.$，
解得2＜m＜3；
②图象与x轴的交点都在x轴的负半轴，
则$\left\{\begin{array}{l}{△≥0}\\{{x}_{1}{x}_{2}=\frac{4m}{m-2}＜0}\\{{x}_{1}{x}_{2}=\frac{2m-6}{m-2}＞0}\end{array}\right.$，
解得：1≤m＜2．
综上可得m的取值范围是：1≤m＜2或2＜m＜3
故选B．
点评 本题考查一元二次方程根的分布与系数的关系以及抛物线和x轴交点的问题，是基础题，难度不大，但不要漏解，解题的关键是注意分类讨论思想的运用．
练习册系列答案
相关题目
1．下列式子中是完全平方式的是（ ）
| A． | a2+2a+1 | B． | a2+2a+4 | C． | a2-2b+b2 | D． | a2+ab+b2 |
19．张先生在上周五（周六周日不开盘）买进了某公司的股票1000股，每股28元．下表是本周每天股票的涨跌情况（单位：元）
求：（1）本周星期三收盘时，每股是多少元？
（2）本周内最高价每股多少元？最低价每股多少元？
（3）已知张先生买进股票时付了0.1%的手续费，卖出时需交了手续费和个人所得税共0.3%，如果张先生在本周末收盘时把全部股票卖出，他的收益是多少元？
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌/元 | +2.8 | +3 | -2 | +1.5 | -2.5 |
（2）本周内最高价每股多少元？最低价每股多少元？
（3）已知张先生买进股票时付了0.1%的手续费，卖出时需交了手续费和个人所得税共0.3%，如果张先生在本周末收盘时把全部股票卖出，他的收益是多少元？
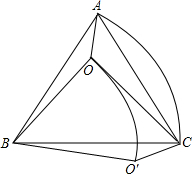如图，O是等边△ABC中一点，OA=2，OB=3，∠AOB=150°，∠BOC=115°，将△AOB绕点B顺时针旋转60°至△CO′B，下列说法中：
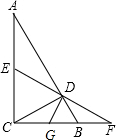如图，△ABC是直角三角形，∠ACB=90°，CD⊥AB于D，E是AC的中点，ED的延长线与CB的延长线交于点F．