题目内容
在进行二次根式化简时,我们有时会碰上如
,
,
一样的式子,其实我们还可以将其进一步化简:
=
=
,
=
=
,
=
=
=
-1,
以上这种化简的方法叫做分母有理化.
还可以用以下方法化简:
=
=
=
=
-1
(1)用不同的方式化简
(2)化简:
+
+
+…
.
| 5 | ||
|
|
| 2 | ||
|
| 5 | ||
|
5×
| ||||
|
| 5 |
| 3 |
| 3 |
|
|
| ||
| 3 |
| 2 | ||
|
2×(
| ||||
(
|
2(
| ||
(
|
| 3 |
以上这种化简的方法叫做分母有理化.
| 2 | ||
|
| 2 | ||
|
| 3-1 | ||
|
(
| ||
|
(
| ||||
|
| 3 |
(1)用不同的方式化简
| 3 | ||||
|
(2)化简:
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
考点:分母有理化
专题:阅读型
分析:(1)利用材料中所给的方法求解即可,
(2)利用分母有理化的方法求解,注意消项.
(2)利用分母有理化的方法求解,注意消项.
解答:解:(1)方法一:
=
=
-
,
方法二:
=
=
=
-
,
(2)
+
+
+…
=
+
+
+…
=
.
| 3 | ||||
|
3(
| ||||||||
(
|
| 10 |
| 7 |
方法二:
| 3 | ||||
|
(
| ||||
|
(
| ||||||||
|
| 10 |
| 7 |
(2)
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
=
| ||
| 2 |
| ||||
| 2 |
| ||||
| 2 |
| ||||
| 2 |
=
| ||
| 2 |
点评:本题主要考查了分母有理化,解题的关键是正确掌握分母有理化的方法.

练习册系列答案
相关题目
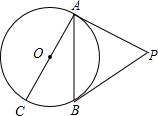 如图所示,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠ACB的度数是( )
如图所示,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠ACB的度数是( )| A、70° | B、40° |
| C、50° | D、20° |
甲、乙两位同学对代数式
(a>0,b>0),分别作了如下变形:
甲:
=
=
-
乙:
=
=
+
关于这两种变形过程的说法正确的是( )
| a-b | ||||
|
甲:
| a-b | ||||
|
(a-b)(
| ||||||||
(
|
| a |
| b |
乙:
| a-b | ||||
|
(
| ||||||||
|
| a |
| b |
关于这两种变形过程的说法正确的是( )
| A、甲、乙都正确 |
| B、甲、乙都不正确 |
| C、只有甲正确 |
| D、只有乙正确 |
二次函数y=-
(x+1)2-1的图象向上平移2个单位后所得的二次函数解析式为( )
| 1 |
| 2 |
A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
 如图,四边形ABCD中,点E、F分别为AB、AD的中点,且EF=3,BC=10,CD=8,求cosC.
如图,四边形ABCD中,点E、F分别为AB、AD的中点,且EF=3,BC=10,CD=8,求cosC. 如图,直线a∥b,c与a,b都相交,∠1=60°,则∠2=
如图,直线a∥b,c与a,b都相交,∠1=60°,则∠2=