题目内容
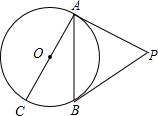如图所示，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=40°，则∠ACB的度数是（ ）| A、70° | B、40° |
| C、50° | D、20° |
考点：切线的性质,圆周角定理
专题：计算题
分析：连接BC，OB，由PA、PB是⊙O的切线，可得∠OAP=∠OBP=90°，根据四边形内角和，求出∠AOB，再根据圆周角定理即可求∠ACB的度数．
解答：解：连接BC，OB，
AC是直径，则∠ABC=90°，
PA、PB是⊙O的切线，A、B为切点，则∠OAP=∠OBP=90°，
∴∠AOB=180°-∠P=140°，
由圆周角定理知，∠ACB=
∠AOB=70°，
故选A．
AC是直径，则∠ABC=90°，
PA、PB是⊙O的切线，A、B为切点，则∠OAP=∠OBP=90°，
∴∠AOB=180°-∠P=140°，
由圆周角定理知，∠ACB=
| 1 |
| 2 |
故选A．
点评：解决本题的关键是连接BC、OB，利用直径对的圆周角是直角，切线的性质，圆周角定理解答．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
如图，是一个被分成6等份的扇形转盘，小明转了2次结果指针都停留在红色区域，小明第3次再转动指针停留在红色区域的概率是判断一个命题是假命题，下列说法正确的是（ ）
| A、要经过严格的推理论证 |
| B、只要举一个符合题设，不满足结论的反例 |
| C、只要举一个既不符合题设，又不满足结论的反例 |
| D、要举若干个反例 |
点（-4，3）关于x轴对称的点坐标是（ ）
| A、（-4，-3） |
| B、（4，3） |
| C、（4，-3） |
| D、（3，-4） |
如图，AB是⊙O的直径，C、D是⊙O上两点，CD⊥AB，若∠DAB=65°，则∠AOC等于（ ）| A、25° | B、30° |
| C、50° | D、65° |
如图，在△ABC中，∠A=80°，∠ABC与∠ACD的平分线交于点E，∠EBC与∠ECD的平分线相交于点F，则∠BFC=抛物线y=-2x2-6x+1的对称轴是（ ）
| A、-3 | ||
| B、x=-3 | ||
C、x=
| ||
D、x=-
|