题目内容

如图，四边形ABCD中，点E、F分别为AB、AD的中点，且EF=3，BC=10，CD=8，求cosC．
考点：三角形中位线定理,勾股定理的逆定理,锐角三角函数的定义
专题：
分析：连接BD，根据三角形的中位线平行于第三边并且等于第三边的一半可得BD=2EF，再利用勾股定理逆定理求出∠BDC=90°，然后根据锐角的余弦等于邻边比斜边列式计算即可得解．
解答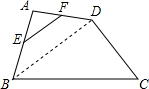：解：如图，连接BD，
∵点E、F分别为AB、AD的中点，
∴EF是△ABD的中位线，
∴BD=2EF=2×3=6，
∵BD2+CD2=62+82=100=BC2，
∴△BCD是直角三角形，∠BDC=90°，
∴cosC=
CD
BC
=
8
10
=
4
5
．
点评：本题考查了三角形的中位线平行于第三边并且等于第三边的一半，勾股定理逆定理，锐角三角函数的定义，熟记定理并作辅助线构造出直角三角形是解题的关键．
练习册系列答案
相关题目
如果函数y=
m-
2
xm2-1
是反比例函数，那么m=
 
．
在平面直角坐标系中，A（2，-3）与点B关于原点对称，则点B的坐标是
 
．
如图，在△ABC中，∠A=80°，∠ABC与∠ACD的平分线交于点E，∠EBC与∠ECD的平分线相交于点F，则∠BFC=
 
．
用“☆”定义一种新运算：对于任意有理数a和b，规定a☆b=
a+b-|a-b|
2
．例如：（-1）☆2=
-1+2-|-1-2|
2
=-1．
（1）计算：（-6）☆（-8）=
 
．
（2）从-
8
9
，-
7
9
，-
6
9
，-
5
9
，-
4
9
，-
3
9
，-
2
9
，-
1
9
，0，
1
9
，
2
9
，
3
9
，
4
9
，
5
9
，
6
9
，
7
9
，
8
9
中任选两个有理数做a，b的值，并计算a☆b，那么所有运算结果中的最大值是
 
．
在进行二次根式化简时，我们有时会碰上如
5
3
， 
2
3
 ， 
2
3
+1
一样的式子，其实我们还可以将其进一步化简：
5
3
=
5×
3
3
×
3
=
5
3
3
 ，
2
3
=
2×3
3×3
=
6
3
，
2
3
+1
=
2×(
3
-1)
(
3
+1)(
3
-1)
=
2(
3
-1)
(
3
)2-12
=
3
-1，
以上这种化简的方法叫做分母有理化．
2
3
+1
还可以用以下方法化简：
2
3
+1
=
3-1
3
+1
=
(
3
)2-12
3
+1
=
(
3
+1)(
3
-1)
3
+1
=
3
-1
（1）用不同的方式化简
3
10
+
7

（2）化简：
1
3
+1
+
1
5
+
3
+
1
7
+
5
+…
1
2n+1
+
2n-1
．
如图，在△ABC中，已知AB=AC，∠B=30°，AB的垂直平分交BC于D，且BD=6cm，求BC的长．
下列做法正确的是（　　）
A、方程
2x-1
3
=1+
x-3
2
去分母，得2（2x-1）=1+3（x-3）
B、方程4x=7x-8移项，得4x-7x=8
C、方程3（5x-1）-2（2x-3）=7去括号，得15x-3-4x-6=7
D、方程1-
3
2
x=3x+
5
2
移项，得-
3
2
x-3x=
5
2
-1
点A（x1，y1），B（x2，y2）为反比例函数y=-
2
x
图象上两点，若y1+y2=
1
x1x2
，则x1+x2的值为（　　）
A、
1
2
B、-
1
2
C、1
D、-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网