题目内容
3.求函数y=x+$\sqrt{-{x}^{2}+10x-21}$的最值.分析 首先求出不等式-(x-5)2+4≥0的解集,进而得出x=5时以及x=3或7时分别求出函数最值即可.
解答  解:∵y=x+$\sqrt{-{x}^{2}+10x-21}$
解:∵y=x+$\sqrt{-{x}^{2}+10x-21}$
=x+$\sqrt{-(x-5)^{2}+4}$,
-(x-5)2+4≥0,
∴如图所示:可得不等式的解集为:3≤x≤7,
故x=5时,y有最大值为:5+2=7,
当x=3或7时,y有最小值为:3.
点评 此题主要考查了无理函数的最值,求出x的取值范围是解题关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
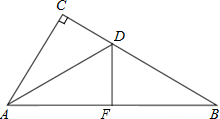 如图,在△ABC中,∠ACB=90°,AD是∠CAB的平分线,△ACD沿AD翻折,C点落在边AB上的点F处.己知AC=6,BC=8,求DF的长.
如图,在△ABC中,∠ACB=90°,AD是∠CAB的平分线,△ACD沿AD翻折,C点落在边AB上的点F处.己知AC=6,BC=8,求DF的长.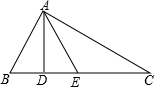 如图,在△ABC中,∠BAC=90°,AD⊥BC,∠BAD=30°,AE为BC边上的中线,求证:AE=AB.
如图,在△ABC中,∠BAC=90°,AD⊥BC,∠BAD=30°,AE为BC边上的中线,求证:AE=AB.