题目内容
16. 如图 在△ABC中,∠B=90° AB=12cm,BC=24cm,动点P从点A开始沿边AB向B以2cm/s的速度移动,动点Q从点B开始沿边BC向C以4cm/s的速度移动. 如果P,Q分别从A,B同时出发 那么△PBQ的面积S随出发的时间t如何变化?写出函数关系式.并指出几秒后△PBQ的面积最大,最大面积是多少?
如图 在△ABC中,∠B=90° AB=12cm,BC=24cm,动点P从点A开始沿边AB向B以2cm/s的速度移动,动点Q从点B开始沿边BC向C以4cm/s的速度移动. 如果P,Q分别从A,B同时出发 那么△PBQ的面积S随出发的时间t如何变化?写出函数关系式.并指出几秒后△PBQ的面积最大,最大面积是多少?
分析 根据两点移动速度以及移动方向得出BP以及BQ的长,进而得出S与t的函数关系式,根据函数的性质求出最值即可.
解答 解:∵动点P从点A开始沿边AB向点B以2cm/s的速度移动.动点Q从点B开始沿边BC向点C以4cm/s的速度移动,
∴设t秒时,△PBQ的面积为S,根据题意得出:
S=$\frac{1}{2}$PB×BQ=$\frac{1}{2}$(12-2t)×4t=-4t2+24t(0≤t<6).
因为S=-4t2+24t=-4(t-3)2+36
所以,3秒后△PBQ的面积最大,最大面积是36cm2.
点评 此题主要考查了二次函数的实际应用,根据面积关系得出函数关系式是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
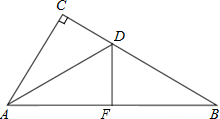 如图,在△ABC中,∠ACB=90°,AD是∠CAB的平分线,△ACD沿AD翻折,C点落在边AB上的点F处.己知AC=6,BC=8,求DF的长.
如图,在△ABC中,∠ACB=90°,AD是∠CAB的平分线,△ACD沿AD翻折,C点落在边AB上的点F处.己知AC=6,BC=8,求DF的长.