题目内容
15.计算:(1)$\frac{2a}{{a}^{2}-4}$-$\frac{1}{a-2}$
(2)$\frac{2x}{{y}^{2}}$•$\frac{2y}{x}$
(3)$\frac{a-1}{{a}^{2}-4a+4}$÷$\frac{{a}^{2}-1}{{a}^{2}-4}$
(4)$\frac{{2{b^2}}}{a+b}$-a+b.
分析 (1)先找出最简公分母,然后通分化简即可.
(2)根据分式的乘法法则即可求出答案
(3)先将分子分母进行因式分解,然后根据分式的乘法法则即可求出答案
(4)先通分,然后根据分式加减运算法则即可求出答案.
解答 解:(1)原式=$\frac{2a}{(a-2)(a+2)}$-$\frac{1}{a-2}$
=$\frac{2a-(a+2)}{(a-2)(a+2)}$
=$\frac{1}{a+2}$
(2)原式=$\frac{4}{y}$
(3)原式=$\frac{a-1}{{(a-2)}^{2}}$•$\frac{(a-2)(a+2)}{(a-1)(a+1)}$
=$\frac{a+2}{(a-2)(a+1)}$
(4)原式=$\frac{2{b}^{2}}{a+b}$-(a-b)
=$\frac{2{b}^{2}-(a-b)(a+b)}{a+b}$
=$\frac{{3b}^{2}{-a}^{2}}{a+b}$
点评 本题考查分式的混合运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
4.式子$\sqrt{3-x}$+$\frac{1}{x-4}$有意义,则x的取值范围是( )
| A. | x≤3 | B. | x≠4 | C. | x≥3或x≠4 | D. | x≤3或x≠4 |
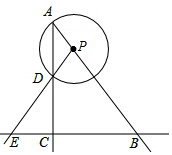 Rt△ABC,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的圆P与射线AC的另一个交点为D,直线PD交BC于点E.
Rt△ABC,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的圆P与射线AC的另一个交点为D,直线PD交BC于点E. 如图,己知AB是半径为2的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.
如图,己知AB是半径为2的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.