题目内容
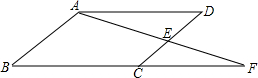如图，在?ABCD中，E为CD的中点，连结AE并延长交BC的延长线于点F，则△ADE与△ABF的面积比为考点：相似三角形的判定与性质,平行四边形的性质
专题：
分析：由平行四边形的性质可证得△ADE∽△FBA，且相似比为1：2，根据相似三角形的性质可求得答案．
解答：解：∵四边形ABCD为平行四边形，
∴AD∥BC，∠B=∠D，AB=CD，
∴∠DAE=∠F，
∴△ADE∽△FBA，
∵E为DC中点，
∴AB=2DE，
∴
=（
）2=（
）2=
，
故答案为：1：4．
∴AD∥BC，∠B=∠D，AB=CD，
∴∠DAE=∠F，
∴△ADE∽△FBA，
∵E为DC中点，
∴AB=2DE，
∴
| S△ADE |
| S△ABF |
| DE |
| AB |
| 1 |
| 2 |
| 1 |
| 4 |
故答案为：1：4．
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．
练习册系列答案
相关题目
如图，在△ABC中，AB=13，AC=15，BC=14，求sinB和sinC的值．
如图，已知一次函数图象交正比例函数图象于第二象限的A点，交x轴于点B（-6，0），△AOB的面积为15，且AB=AO，求正比例函数和一次函数的解析式．
如图，线段AC、BD交于点M，过B、D两点分别作AC的垂线段BF、DE，
已知：如图，AB∥CD，AB=CD，点B、E、F、D在同一直线上，∠A=∠C．
如图，AB是⊙O的切线，切点为B，AO交⊙O于点C，过点C作DC⊥OA交AB于点D
如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=6，点D是边BC的中点，点E是边AB上的任意一点（点E不与点B重合），沿DE翻折△DBE使点B落在点F处，连接AF，则线段AF长的最小值是
如图，在△ABC中，∠C=90°，∠BAC=60°，AC=1，点D在BC上，点E在AB上，使得△ADE是等腰直角三角形，∠ADE=90°，求BE的长．（提示：可以运用“直角三角形中，30°角所对的直角边等于斜边的一半”）．